A Model with Dopamine Depletion in Basal Ganglia and Cerebellum Predicts Changes in Thalamocortical Beta Oscillations
Abstract
Parkinsonism is presented as a motor syndrome characterized by rigidity, tremors, and bradykinesia, with Parkinson’s disease (PD) being the predominant cause. The discovery that those motor symptoms result from the death of dopaminergic cells in the substantia nigra led to focus most of parkinsonism research on the basal ganglia (BG). However, recent findings point to an active involvement of the cerebellum in this motor syndrome. Here, we have developed a multiscale computational model of the rodent brain’s BG–cerebellar network. Simulations showed that a direct effect of dopamine depletion on the cerebellum must be taken into account to reproduce the alterations of neural activity in parkinsonism, particularly the increased beta oscillations widely reported in PD patients. Moreover, dopamine depletion indirectly impacted spike-time-dependent plasticity at the parallel fiber-Purkinje cell synapses, degrading associative motor learning as observed in parkinsonism. Overall, these results suggest a relevant involvement of cerebellum in parkinsonism associative motor symptoms.
1. Introduction
Parkinsonism is a set of movement symptoms associated with Parkinson’s disease (PD) resulting from the degeneration of dopaminergic neurons in the substantia nigra pars compacta (SNc).1,2 This reduces dopamine levels in the basal ganglia (BG), modifying local circuit computation, and eventually altering thalamocortical activity. As a result, cortical oscillations in the ββ-band (13–30 Hz) increase, providing a reliable clinical marker of the motor state in Parkinsonian patients.3,4,5,6,7
While the role of BG in parkinsonism has been intensely investigated, recently the cerebellum has also been implicated in the disorder’s pathophysiology.8,9,10 Cerebellar functions and morphology have been shown to be altered in both human11 and animal12 parkinsonism studies. However, it is not clear how the loss of SNc dopaminergic neurons might affect cerebellar dynamics and impact the disease.
A recent hypothesis is that the equilibrium of the cerebellar microzones (i.e. functionally defined longitudinal strips of cerebellar cortex13,14,15) might be modified by the dopaminergic loss in parkinsonism. This hypothesis is supported by the presence of dopaminergic inputs from SNc and the expression of dopamine receptors in the cerebellum.16 The cerebellum also generates a feedback pathway to dopaminergic nuclei projecting to the ventral tegmental area17,18 or the substantia nigra pars reticulata (SNr)19 exploiting its predictive capabilities to regulate the reward system. Therefore, the relationship of the cerebellum with the dopaminergic system and the BG is bidirectional. The cellular apoptosis and reduced activity of the cerebellar cortex in parkinsonism animal models12,20 could be instrumental for a cerebellar role in PD.
Indeed, there is a di-synaptic connection originating from the subthalamic nucleus (STN) and terminating in the cerebellar cortex via the pontine nucleus,21 thanks to which the synchronous ββ-band oscillations originating from the BG could drive the cerebellum out of its physiological ranges.22,23,24
Notably, dopaminergic treatments may enhance cerebellar pathological changes, which are reported to reduce the active dopamine receptor levels in cerebellum.25 Each of these factors may cause modifications of the Parkinsonian cerebellum, and further investigation is needed to understand their relative influence.
Another explanation for the altered cerebellar activity in parkinsonism may be attributed to cerebellar compensation to maintain brain activity. Indeed, in the early stages of the disorder, patients demonstrated proficient performance in motor tasks despite exhibiting cerebellar hyperactivation in BOLD signal studies.26,27 Such increase could be explained by a compensation via the cerebello-thalamocortical loop for the lower striato-thalamocortical circuit activity,28 and these compensatory effects may remain effective until around 70% of the SNc dopaminergic neurons have degenerated.29
Remarkably, pathological and compensatory effects may represent the causes of different clinical symptoms in parkinsonism. Since akinesia and rigidity are rapidly overcome by dopaminergic treatments, they might be induced by the aberrant BG drive on the cerebellum (e.g. Abulikemu et al.30 showed that levodopa modifies the cerebellum-BG direct pathway). Conversely, tremor might emerge through different mechanisms: the current hypothesis (i.e. the “dimmer-switch” model31) formulates that, while BG may trigger the tremor, the cerebellum (specifically the cerebello-thalamocortical loop) amplifies tremor amplitude. Whether this is caused by compensation or pathological changes in the circuit still needs to be investigated. Unfortunately, these findings reflect a relatively recent interest in the cerebellar involvement in parkinsonism, leaving the mechanisms behind such altered activity unclear, hindering the development of more effective pharmacological treatments and neurostimulation treatments.32
Given the impracticality of investigating multiple circuit interactions in vivo, our study adopts a computational approach to explore the pathological mechanisms underlying alterations in cerebellar activity observed in experimental studies. Specifically, we developed a multiarea — with different levels of details — multiarea — multiple brain areas — model encompassing brain regions predominantly implicated in parkinsonism and simulated the electrophysiological hallmarks of this condition.
This computational strategy offers distinct advantages over traditional experimental methods. It allows for the examination of complex systems that are challenging to study directly and facilitates hypothesis testing and prediction generation. Our model was designed to simulate the effects of dopamine depletion in spiking neural networks (SNNs). The model included interconnected components, as shown in Fig. 1. To achieve this, the study adapted and incorporated highly biologically plausible spiking models from previous studies for the cerebellar33 and BG34 networks, since these regions were the focus of the investigation. Mass models were also used for the thalamus, thalamic reticular nucleus, and cortex, adapting the work by Yousif et al.35 SNNs simulate the behavior of single neurons,36 while mass models describe the dynamics of neuronal ensembles.37 By combining these models, we have created a computational tool balancing biological plausibility against the computational burden to examine the interplay between cerebellum and BG in parkinsonism.
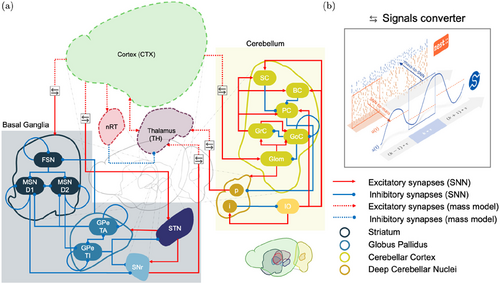
Fig. 1. (Color online) Network architecture. Panel (a) illustrates the connection diagram of the simulated network. The BG (whose subpopulations are represented in different shades of blue) and the cerebellum (shades of yellow) were modeled using SNNs, while the cortex (CTX), the thalamus (TH), and the thalamic reticular nucleus (nRT) were simulated via mass models (indicated by dashed lines). Custom software interface (panel (b)) was developed to integrate SNNs and mass models in a multiscale architecture. At each time step of one simulation, output spikes of SNNs are converted to firing rates with a windowed average and given as input to the corresponding mass models. In contrast, mass models’ output firing rates are used as Poisson distribution parameters to compute input spike trains for the connected SNNs. During closed-loop simulations, both the BG and the cerebellum receive external inputs (not shown in the figure for the sake of clarity) that implicitly mimic the external brain areas’ activity; such inputs target GPe-TI, GPe-TA, SNr, and Glom. List of abbreviations: FSN: Fast-spiking Neurons; MSN-D1: Medium Spiny Neurons, Dopamine 1 receptors; MSN-D2: Medium Spiny Neurons, Dopamine 2 receptors; GPe-TA: external Globus Pallidus, Type arkypallidal; GPe-TI: external Globus Pallidus, Type prototypical; STN: Subthalamic Nucleus; SNr: Substantia Nigra pars reticulata; Glom: Glomeruli; GrC: Granule Cells; GoC: Golgi Cells; PC: Purkinje Cells; BC: Basket Cells; SC: Stellate Cells; IO: Inferior Olive; p: Projecting deep cerebellar nuclei cells; i: Inhibitory deep cerebellar nuclei cells.
Our objective was to investigate whether the effects associated with dopamine depletion in both the cerebellum and BG contribute to specific pathological features observed in parkinsonism. To achieve this, we made adjustments to properties concerning network topology and neuronal models within these regions. Subsequently, we analyzed how these alterations influenced the temporal and frequency characteristics within the thalamocortical loop. Notably, our study’s innovation lies in our approach of not imposing constraints on the beta band, the frequency range we aimed to test. Instead, we focused solely on modifying the model within the SNN. Our primary finding was the alignment of our results with experimental observations in the mass models, particularly regarding frequency content behaviors within the thalamocortical loop. This highlights the significance of incorporating biologically derived alterations, demonstrating their ability to replicate experimental findings and potentially advancing our understanding of parkinsonism.
In the following sections, we will initially introduce the models from existing literature that were employed in this study, covering both the SNN areas33,34 in Secs. 2.1 and 2.2 and the mass models.35 in Sec. 2.3 Following that, we will present the integration (Sec. 2.4), optimization (Sec. 2.5), and testing (Sec. 2.6) procedures applied to analyze the role of dopamine depletion in these loops and the involvement of the cerebellum in parkinsonism. We will then present the obtained results and discuss them. Lastly, we will compare our model with other existing works and report this study’s limitations and possible future developments.
2. Materials and Methods
2.1. Basal ganglia network
The first of the two spiking components, namely the BG SNN, was implemented following a previous work Lindahl and Kotaleski34 that reports detailed neuron and synapse equations. Additionally, in formulating the model, the authors included and validated against experimental observations a parameter to define the dopamine depletion level, making it particularly suitable for this study.
The quantitative computational model of the BG includes the striatal subnetwork, the external Globus Pallidus (GPe), the STN, and the output nucleus, the SNr. In the striatum, the projection neurons [medium spiny neurons (MSNs)] are controlled by the inhibition coming from fast-spiking neurons (FSNs) and external Globus Pallidus type A neurons (GPeTA). The model includes dopaminergic neurons in the SNr, projecting to striatal neurons and modulating the activity of the entire BG network. Point neuron models were used to ensure a good trade-off between simulation efficacy and biological plausibility: quadratic integrate and fire models with adaptation38 for FSN and MSN, and adaptive exponential integrate and fire models39 for the remaining components of the network. Using this formalism, the membrane potential of each neuron in the BG network is described by a set of differential equations that capture the temporal evolution of the voltage guided by the opening and closing of ion channels in the membrane.
Ultimately, this computational model allows the simulation of dopamine depletion mechanisms, whereby the impact of disease progression can be effectively captured by modeling the prominent shifts in both cellular and topological properties of the neural network (for a full description of the dopamine-related changes, see the work by Lindahl and Kotaleski34 or the supplementary file in the Zenodo repository Sec. 5). This is achieved by including a continuous parameter ξξ, representing the variation of bounded dopamine receptors with respect to the physiological state (ξξ values range from ξ=0ξ=0, healthy control, to ξ=−0.8ξ=−0.8, severe PD, with 80%80% of dopamine receptors unbounded compared to the physiological state).
2.2. Cerebellar network
The second spiking component of the loop, the cerebellum SNN, was adapted from the work by Geminiani et al.33 The original model consists of a 3D reconstruction of the olivocerebellar microcircuit, which incorporates optimized neuronal models and morphologically derived topology.40 The 3D reconstruction results in a model including 96,767 neurons and 4,151,182 total synapses, replicating two microzones with their respective olivary nuclei. The model employs Extended-Generalized Leaky Integrate and Fire (EGLIF) point neuron models to simulate neural dynamics and express the main features of cerebellar neurons.41 Although the original 3D extension of the cerebellar microcircuit is not preserved here (our simulation platform is a-dimensional in terms of spatial network organization), the overall structure and connectivity of the network are equivalent to the ones in Geminiani et al.33
Such a computationally lightweight model of the cerebellar network includes the three main cerebellar cortical layers as well as the deep cerebellar nuclei (DCN) and the inferior olive (IO) neurons. The network receives external inputs via the mossy fibers to glomeruli (Glom) in the granular layer, which connect to granule (GrC) and Golgi (GoC) cells. The subsequent layers include the Purkinje Cells (PCs) and molecular interneurons [namely Basket (BC) and Stellate Cells (SCs)].
PCs receive inputs from the GrCs, both BCs and SCs interneurons, and teaching signals from IO neurons, and in turn, modulate the output of the whole microcircuit through their inhibitory effect on the glutamatergic projecting neurons of the deep cerebellar nuclei (DCNp). The IO neurons are regulated by an inhibitory loop with the GABAergic deep nuclei (DCNi), which control the synchrony and timing of the teaching signal.42
As the goal of this study was to adopt the multiarea model for investigating the role of the cerebellum in the pathophysiology of parkinsonism, we extended the original cerebellar model with a mechanism to account for progressive dopamine depletion based on literature findings. Previous studies have indeed suggested that cerebellar cells express dopamine receptors,16 and atrophy of the PC layer has been observed when mimicking the effects of dopaminergic cell loss in mice.20 To simulate this effect, we incorporated a simple mechanism of PC apoptosis in the cerebellar model: specifically, we modeled a linear reduction of PC numerosity proportional to the same parameter ξξ used in the BG SNN,34 with a value of ξ=0ξ=0 corresponding to the full PC population, ξ=−0.8ξ=−0.8 corresponding to advanced PD. This last case compares well to the 50% PC reduction suggested by a reduction of firing activity in half of the monitored PC following dopaminergic lesion.12
2.3. Thalamocortical mass models
The remaining areas were modeled using a simplified approach, allowing us to include plausible physiological connections between the detailed cerebellum and the BG SNNs while maintaining a low computational cost.
For this purpose, we adapted the model composed of seven ordinary differential equations proposed by Yousif et al.,35 which describes the temporal dynamics of a cerebellar-BG thalamocortical network.
The differential equations are formulated based on the Wilson–Cowan approach,37 and can be represented in a compact matrix form (Eq. (1))
In this mathematical formulation, the nth component of x (xn) represents the number of active neurons in the nth population. Its temporal evolution can be written, following the first equation, as
The temporal evolution of the nth population is thus characterized by a set of constants (namely kn, βn, and θn), which take different values depending on whether the population is excitatory or inhibitory: ke=0.9945, βe=1.3, θe=4.0 or ki=0.9994, βi=2.0, and θi=3.7.35 Finally, τ is a time constant and has the same value (10ms) across all populations.
Since both BG and cerebellum are represented by SNN models (hence represented with a more biologically plausible approach), these areas are not included in the system with their own state equations, as in Yousif et al.,35 but rather their outputs are fed to the model as exogenous inputs.
With these premises, our nonlinear time-invariant system resulted in three differential equations (Eq. (3)), one each for cortex, thalamus, and thalamic reticular nucleus.
The state variables array includes activities from the cortex, thalamus, and thalamic reticular nucleus (x=(xCt xT xn)T), while the inputs from the spiking models are the action potentials of SNr and DCNp neurons (u=(uSNr uDCNp)T).
The weights of the connection are encompassed in sparse matrices where only four parameters for ai,j, and two for bi,j are different than zero, accounting for the connectivity among areas in the model.
Furthermore, the cortex is the only area projecting to BG and cerebellum: its activity, xCt, modulates the frequency of input spike trains to the kth spiking population (yk), according to the corresponding connection weight, ck,Ct.
The nonzero weights of the inter-area connections ai,j were replicated from the original model. At the same time, bi,j and ck,Ct were optimized using a genetic algorithm (see Sec. 2.5).
2.4. Multiscale simulation handler tool
Since the mathematical formulation and the software libraries to simulate SNNs and mass models are different (as they operate on distinct scales of resolution), the inputs and outputs of these two classes of models needed to be converted in real-time during simulations to allow neural activity to be transmitted between the different areas in the proposed multiscale network.
To that end, we implemented a custom conversion tool to handle and combine the different signals during simulations, as shown in Fig. 1(b): each simulation is iteratively stopped every period T to let the SNN and mass models exchange information and set the inputs for the following period, T+1. The instantaneous firing rate from the output SNN population is evaluated as the average number of spikes per second per neuron and becomes the input to the mass model system. On the other hand, the system’s output y is used as the instantaneous firing rate of input spike trains to the connected spiking populations, implemented as Poissonian processes with mean y.
We based our implementation on a similar dedicated solution which has already been proposed in the “The Virtual Brain” (TVB) framework,43 in the context of managing co-simulation between the TVB, a mass model simulator, and NEST, an SNN simulator. The user can set the integration period T, balancing the trade-off between simulation time and results accuracy. We set T to 1 and 10 ms in the different cases when we needed, respectively, higher resolution or lower computational load (i.e. the simulation of learning protocols).
2.5. Inter-area connectivity optimization
After defining all the components of the network described above, an optimization process was carried out to fine-tune the weights of the connections between the different areas. The optimization process was carried out through a genetic algorithm specifically designed to minimize the discrepancies between the activity of the multiarea circuit and the results achieved in their corresponding studies, using the following fitness function:
The first two terms of the fitness function are proportional to the Euclidean norm of the difference between the average firing rates of the SNN within the closed-loop model and those observed in stand-alone microcircuits, specifically for the cerebellum33 and the BG34 (frCrb−frCereb,ref. and frBG−frBG,ref.), weighted by the inverse of the standard deviations Sσ of the mean firing rates. Since their contribution is considered as a negative term, the more discrepancy the model shows, the lower the fitness function; hence the maximum of Jfitness is found when such differences are closer to zero.
The stand-alone SNNs were first simulated in a state of nonspecific motor activity lasting for 3 s: the BG were simulated in an “active” state, as defined in the reference study,34 while the cerebellum was simulated with a Poissonian activity of mean firing rate of 36 Hz given as input, thus using the values reported as conditioned stimulus (CS) in the original paper in order to simulate a cerebellar hyperactivation.33
To avoid overfitting, we relaxed the optimization constraints to only take into account the firing rates from the most informative spiking populations instead of all of them: in particular, the cerebellar populations considered were Glom, DCNp, and PCs, while for the BG, the nuclei taken into account were GPe, STN, and SNr.
Since it was not possible to identify specific reference values for the activity of mass models to be compared with (as the cortical areas have a wide, context-based oscillation regime), the third term of the function expresses the ability of the mass models to reproduce the thalamocortical γ-band healthy oscillations (>30 Hz),44 which were also sought to be reproduced in Yousif et al.35 To do so, Jfitness was designed to include the integral of the wavelet transform power of the thalamic WT activity in the frequencies 30–50 Hz, modulated by a Gaussian window G (with mean=40 Hz, SD=6 Hz), which increases proportionally to the amount of spectral energy of the signal in the γ-band.
Once the target values were collected as a reference, the algorithm sought the best combination of connection weights that maximized the fitness function Jfitness by iteratively testing different sets of parameters until a convergence towards the maximum was found. In particular, the genetic algorithm was implemented using the PyGAD library45 with the following settings: five generations, two parents selected for mating in each generation, a population size of two candidate solutions evaluated per generation, each candidate solution consisting of four genes. The parent selection method employed was steady-state selection, with a random mutation type applied to each gene with a 50% probability. Crossover was performed using a single-point method, and no specific stopping criteria were defined.
2.6. Testing protocols
Having set up the model to reproduce healthy conditions, to investigate the role of dopamine depletion in the multiarea multiscale model, two testing protocols were conducted in two different conditions of dopamine depletion: simulating dopaminergic effects in the BG only and in both cerebellum and BG.
2.6.1. Protocol 1: Active state
We first aimed to examine the effects of dopamine depletion within an active motor state. To achieve this, we repeatedly simulated the multiarea circuit at five levels, from physiological to increasing parkinsonism severity (ξ=[0,−0.1,−0.2,−0.4,−0.8]). Specifically, the circuit was simulated 10 times for a period of 3 s across the two dopaminergic conditions (only in BG and both cerebellum and BG).
2.6.2. Protocol 2: Eyeblink classical conditioning
The second set of testing protocols aimed at investigating the functional performance of the circuit under both physiological and dopamine-depleted conditions using an associative learning protocol. In fact, we sought to investigate the impact of dopamine depletion on learning and plasticity within the cerebellum in a closed-loop setting.46 To do so, we incorporated a spike timing-dependent plasticity (STDP) mechanism in the cerebellum SNN in the connection between the parallel fiber and Purkinje Cells (pf-PC)46 and simulated an eyeblink classical conditioning (EBCC) protocol. Hebbian STDP enacts the fundamental cause-and-effect relationship proposed by Hebb’s theory. It reinforces synapses activated before post-synaptic spikes and weakens synapses activated after post-synaptic spikes, aligning with Hebb’s principle of synaptic plasticity.47 The EBCC protocol involves the association of a neutral CS with an unconditioned stimulus (US), resulting in the acquisition of a conditioned response (CR) to the CS alone.48
The simulated EBCC experiments consisted of 100 trials of 580 ms, in which the cerebellum SNN received cortical noise at 4 Hz throughout the whole trial, on top of which a complex stimulus at 36 Hz was administered between 100 and 380 ms. Additionally, the cerebellum would receive a teaching signal from the IO at 200 Hz in the 350–380 ms window, co-terminating with the CS.49
2.7. Data analysis
2.7.1. Protocol 1: Active state
The behavior during a state of nonspecific motor activity was assessed by analyzing both temporal and frequency features. The main temporal feature calculated was the mean firing rates (¯fr) of the spiking models, which summarize populations’ activity over time. According to Johnson50¯fr can be calculated as follows :
To obtain the frequency features of the signal, first, the signals were converted into the frequency domain using wavelet decomposition and subsequently the “Fitting Oscillations and One-Over F” (FOOOF) technique51 was used to separate the periodic and aperiodic components of the power spectrum. Using this technique, the aperiodic term can be described by the hyperbolic function c1fk: first, the numerical values of the parameters k and c were estimated using the Python package provided by Donoghue et al.51 alongside the paper describing the technique (the FOOOF tool). Then, these components were removed to focus exclusively on the periodic peaks in the spectrum.
Furthermore, we aim to characterize better the emergence of synchronous oscillations in the mass models. To do so, the phase differences between mass models’ activities and the corresponding circular variance values (CV) were calculated.52 The original time series were filtered with a band-pass filter between 13–30 Hz to keep the beta band components only. Then, the phase values ϕ(t) of filtered signals were computed from their Hilbert transforms, and pair-wise instantaneous phase differences were calculated for the three mass models in the three dopamine depletion sites (i.e. at time t=ˆt, Δϕctx-thal,site(ˆt)=ϕctx,site(ˆt)−ϕthal,site(ˆt)).
2.7.2. Protocol 2: Eyeblink classical conditioning
To evaluate the performance of the model during the EBCC, we monitored the activity of two key neuronal populations, PCs and DCN, as they underwent well-established firing changes driven by plasticity. In particular, we assessed both their intrinsic firing properties, such as firing rate, and their firing modulation, by computing the Spike Density Function (SDF). This method involves convolving individual cells’ spike trains with a kernel function, a Gaussian function of 20 and 10 ms for PCs and DCN, respectively,53 to effectively blur the firing rate estimate over time. This smoothing helps to reduce the effects of random fluctuations in the spike count and provides a more reliable estimate of the underlying firing rate. The SDFs of the neurons within each of the two populations were averaged to obtain the population’s overall SDF.
We also derived the output response (the CR, i.e. eyelid closure) by applying a moving average filter with a 100 ms time window to the DCN population SDF to quantify learning further. This was due to taking into account the transformation of neural signals into effective eyelid movements. A CR was detected when the output signal reached a fixed threshold of 6.2 Hz in the CR time window and remained above the threshold. The threshold value was selected to have a curve comparable to the one obtained by Geminiani et al.49 In this way, each trial corresponds to a Boolean variable of success or failure. Lastly, to have a comprehensive measure, we computed the percentage of CRs (%CR) in each block of 10 trials.54,55
2.8. Implementation details
The SNN microcircuits were implemented in Python 3.8, exploiting the PyNEST API to reconstruct and simulate the networks.56 To allow proper integration of the models, both the BG (originally implemented using NEST Simulator 2.12) and the cerebellar models ( NEST Simulator 2.18) were ported to NEST Simulator 2.20.2. Furthermore, the mass models’ implementation by Yousif et al.35 was then replicated in Python using the Scipy’s odeint routine from its original definition in MATLAB. Simulations were performed on a tower computer (64 GB of RAM, Intel(R) Core(TM) i9 CPU 12th Gen) running Ubuntu OS 20.04.5.
3. Results
This section will initially outline the results derived from the optimization process under physiological circumstances. Following that, we will present the simulation results and the observations acquired under pathological conditions, starting with the nonspecific motor state (referred to as active state), and concluding with the results of the EBCC.
3.1. Multiarea circuit activity in physiological conditions
The two spiking networks of the multiarea circuit (cerebellum and BG) had been tuned and validated against in vivo data in independent studies.33,34 Here, we validated the SNNs embedded in the loop using the parameters reported in the original SNN simulations.
In vivo, the activity of each brain area is influenced by the activity ongoing in the other areas to which it is (directly or indirectly) connected. Hence, when conducting single-area validations of BG and cerebellum, the impact of other brain areas is indirectly incorporated by how they influence the firing rate of BG and cerebellum networks. In fact, the parameters in the multiarea circuit were adjusted to mimic the firing rates of the BG and cerebellum SNNs, thereby establishing an overarching constraint on the entire multiarea circuit at a global, high-level scale (Fig. 2 and Table 1).
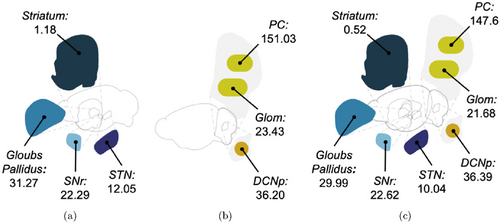
Fig. 2. Comparison between firing rates of SNN populations as in stand-alone models and multiarea network mean firing rates values (in Hz) of SNN populations in the closed-loop configuration (panel (c)) and when taken individually: BG only in panel (a)34 and cerebellum only in panel (b).33
| Population | Variation [Hz] |
|---|---|
| DCNp | 0.19 |
| PC | 3.4 |
| Glom | 1.75 |
| GPe | 1.27 |
| SNr | 0.33 |
| STN | 2.01 |
| Striatum | 0.65 |
3.2. Protocol 1: Active state
To investigate the impact of cerebellar dysfunction in parkinsonism on motor processing (in both the temporal and frequency domain), associative motor learning, and plasticity, we first considered two different pathological hypotheses: dopamine depletion in BG only 34 and dopamine depletion in both cerebellum and BG. The impact of these different sites of dopamine depletion on network activity was compared by evaluating the mean activity of each population in the temporal domain (Fig. 3), as well as in the time-frequency domains by analyzing wavelet transforms (Fig. 4) and phase coherence.
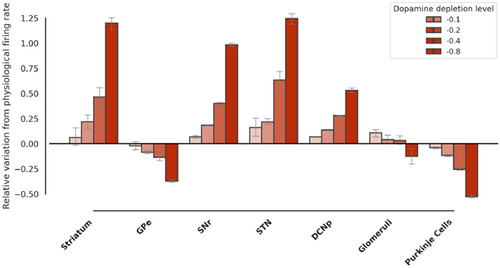
Fig. 3. Closed-loop simulations — firing rate variations with respect to dopamine depletion level: histograms of normalized firing rate variations in the main spiking populations. Simulations with dopamine depletion in cerebellum + BG varying the level of the depletion parameter (ξ), i.e. throughout the progression of the pathology.
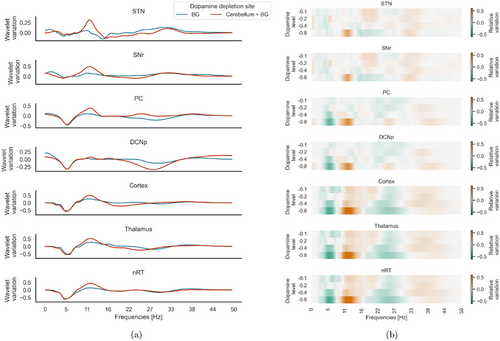
Fig. 4. (Color online) Spectral analysis in different dopamine depletion sites: spectrum values of the three mass models (cortex, thalamus, nRT), the SNr, STN, PC, and DCNp. In panel (a), each curve represents the variation of the power spectrum under different sites of dopamine depletion [the BG (blue) and both cerebellum and BG (red)] evaluated at the most severe case (ξ=−0.8) with respect to the physiological condition (ΔWT=WT pathological−WT physiologicalWT physiological). In panel (b), the heatmap shows the variation of the power spectrum in the case of different magnitudes of dopamine depletion (ξ=−0.1,−0.2,−0.4,−0.8) in both BG and cerebellum.
In Table 2, a comparison detailing the variations in firing rates (Δ) within the spiking population is presented, contrasting the multiarea models against experimental observations. This comparative analysis proves challenging due to the considerable variability evident in the average recorded rates from the experimental studies.
| Model | |||||
|---|---|---|---|---|---|
| BG | Cerebellum + BG | Experiment | Refs. | ||
| Striatum | Δ[%] | 38 | 113 | 722 | Ref. 57 |
| frphysiological[Hz] | 0.55 ± 0.06 | 0.82 ± 0.61 | Ref. 57 | ||
| frpathological[Hz] | 0.75 ± 0.05 | 1.16 ± 0.04 | 6.64 ± 2.83 | Ref. 57 | |
| GPe | Δ[%] | −38 | −37 | −10 | Ref. 58 |
| −40 | Ref. 59 | ||||
| frphysiological[Hz] | 29.75 ± 0.72 | 30.4 ± 11.4 | Ref. 58 | ||
| 33.7 ± 1.3 | Ref. 59 | ||||
| frpathological[Hz] | 18.42 ± 1.16 | 18.8 ± 0.52 | 27.3 ± 9.8 | Ref. 58 | |
| 20.2 ± 0.5 | Ref. 59 | ||||
| STN | Δ[%] | 102 | 131 | 56 | Ref. 60 |
| 107 | Ref. 59 | ||||
| 72 | Ref. 58 | ||||
| 84 | Ref. 61 | ||||
| frphysiological[Hz] | 9.77 ± 0.78 | 2.21 ± 0.22 | Ref. 60 | ||
| 15 ± 2.5 | Ref. 59 | ||||
| 11.8 ± 9.1 | Ref. 58 | ||||
| 9.4 ± 0.8 | Ref. 61 | ||||
| frpathological[Hz] | 19.7 ± 0.89 | 22.6 ± 0.73 | 3.45 ± 0.3 | Ref. 60 | |
| 31 ± 2.5 | Ref. 59 | ||||
| 20.3 ± 9.3 | Ref. 58 | ||||
| 17.3 ± 2.6 | Ref. 61 | ||||
| SNr | Δ[%] | 102 | 101 | −2 | Ref. 62 |
| 54 | Ref. 63 | ||||
| frphysiological[Hz] | 22.3 ±0.59 | 30 ± 6.14 | Ref. 62 | ||
| 2.11 ± 0.77 | Ref. 63 | ||||
| frpathological[Hz] | 42.5 ± 1.57 | 44.9 ± 0.42 | 29.27 ± 3.84 | Ref. 62 | |
| 3.25 ± 1.59 | Ref. 63 | ||||
| DCNp | Δ[%] | 4 | 54 | 101 | Ref. 12 |
| frphysiological[Hz] | 36.1 ± 0.69 | 9.6 ± 5 | Ref. 12 | ||
| frpathological[Hz] | 37.7 ± 0.42 | 55.7 ± 1.06 | 19.3 ± 9.2 | Ref. 12 | |
| PC | Δ[%] | −22 | −53 | −36 | Ref. 12 |
| frphysiological[Hz] | 148.3 ± 2.10 | 43.1 ± 7.41 | Ref. 12 | ||
| frpathological[Hz] | 85.5 ± 0.78 | 69.6 ± 2.44 | 27.4 ± 8.48 | Ref. 12 | |
| Glom | Δ[%] | −69 | −14 | −51 | Ref. 12 |
| frphysiological[Hz] | 22.03 ± 1.48 | 0.96 ± 0.88 | Ref. 12 | ||
| frpathological[Hz] | 6.78 ± 0.77 | 19.0 ± 2.01 | 0.47 ± 0.39 | Ref. 12 | |
In particular, we compared our model results both in the case of dopamine depletion only in the BG and in both cerebellum and BG to experimental data.
Notably, both models demonstrate an intriguing capability to mimic the trends of these changes across all populations.
However, determining which dopamine depletion site configuration better quantitatively reflects experiments is not straightforward and highly area-dependent. Particularly, the cerebellum + BG configuration exhibits a Δ closer to experimental data in the striatum and the DCNp, despite differences in absolute values. Conversely, other areas, such as PC, Glom, and STN, suggest the opposite trend, where the BG only condition appears to be closer, although absolute values vary widely across experiments.
Ultimately, for GPe and SNr, both settings yield similar firing rates and Δ values: SNr is somewhat more distant from experimental values, yet considering the high variability in the experiments, while GPe aligns particularly well with data from Mallet et al.59
Additionally, it should be noted that the model changes gradually with the intensity of the dopaminergic damage [Pearson correlation R ranging from 0.97 to 0.99, p-values <0.05 for all SNN populations (N = 20, for each population), with striatum, SNr STN, DCNp positively correlated and GPe, Glom, and PC negatively correlated], akin with the concept that the disease is proportional to the severity of the pathological change in firing rates (Fig. 3). Therefore, adding dopaminergic cerebellar mechanisms to Parkinsonian models can improve their descriptive capacities compared to models focusing on the BG alone.
After a thorough temporal analysis of the closed-loop model, we further investigated the underlying neural mechanisms in the frequency domain.
The power spectrum variation with respect to the physiological condition was calculated in the two different conditions of interest, i.e. with dopamine depletion in only BG and in both cerebellum and BG (the maximum depletion value is simulated) (Fig. 4(a)). We then evaluated the effect of increasing dopamine depletion at both BG and cerebellum (Fig. 4(b)).
Simultaneous dopamine depletion in the cerebellum and BG led to a most pronounced peak in the beta band, compared to dopamine depletion in BG only: the relative increase, indicated as median (IQR), of the maximum value in the 13–30 Hz band from BG only condition to cerebellum and BG condition is 0.33(0.16) in the cortex, 0.30(0.20) in the thalamus, 0.39(0.08) in the nRT, 0.40(0.16) in the STN. Differences between conditions were tested with the Mann–Whitney test and resulted in p-values <0.01 for all areas, N=5 for each population (Fig. 4(a)). Interestingly, dopamine depletion in the cerebellum only caused a decrease in power spectrum across all frequency values in most areas, except for the STN (Fig. A.1).
Alongside the elevation observed in the beta band, a reduction in theta band power is evident across the cerebellum, cortex, and thalamus, consistently observed across all depletion site configurations.
Lastly, we analyzed the circular variance to further elucidate the emerging synchrony between time-varying signals in the β-band. Simulations revealed that stronger cortico-thalamic synchronization (i.e. a higher Circular Variance) was achieved when dopaminergic effects were modeled in both the cerebellum and BG (CVBG=0.132, CVcerebellum+BG=0.191, see Fig. B.1 in Appendix B).
3.3. Protocol 2: EBCC
EBCC was simulated to investigate the effects of dopamine depletion on associative motor learning and plasticity in the cerebellum by incorporating a mechanism for STDP in the pf-PC connection.46
According to Fig. 5, we focused the EBCC protocol on the model with the highest impact of dopamine effects, i.e. with depletion affecting both BG and cerebellum. Simulations were performed with different degrees of dopamine depletion, comparing the learning performance to that obtained under physiological conditions. The same analysis results obtained using dopamine depletion in BG only or in cerebellum only are presented in Appendix C.
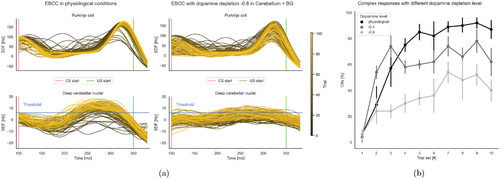
Fig. 5. Learning protocol: EBCC results both in terms of activities of the main populations of interest (PCs and DCNp) and in terms of %CR. Panel (a) shows the results of the EBCC protocol under both physiological (left panel) and dopamine-depleted (right panel) conditions. The entire CS window is shown, with all trials overlaid (each curve represents the SDF within a single trial, and the trials’ progression is shown with a shaded color). The signals are adjusted for the baseline evaluated in the 200 ms following the stimuli. US start and threshold for identification of CR are reported. In panel (b), the percentage of CR identified in each 10-trial block at different magnitudes of dopamine depletion ξ (0 = physiological state, −0.4, −0.8).
In physiological conditions (on the left in Fig. 5(a)), we observed an initial potentiation coinciding with the start of the CS, followed by a gradual depression towards the end of the CS (due to long-term depression) that anticipates the onset of the US, corresponding to a decrease of 36.8(3.59) Hz (N=5) between the averaged activity of the first 10 trials and the last 10 trials in the 280–380 ms window. This behavior is reflected in the DCNps, which are progressively released from PCs inhibition along the trials, anticipating the response and exceeding the threshold that activates the CR.
In the pathological case (on the right in Fig. 5(a)), two main effects on PCs and DCNps were observed. On the one hand, the PC input showed higher variability, and the learning was less marked, corresponding to a decrease of 29.9(4.45) Hz (N=5). This was caused by the reduced drive caused by the dopamine depletion at the BG level and reflected in a reduced cortical input to the cerebellum and by dopamine depletion in cerebellum that reduced the number of healthy PCs. On the other hand, the output from the DCNps was reduced because of the reduced drive from the cortex via the mossy fibers. Finally, we quantified the CR rate, i.e. the performance of the cerebellum in anticipating the response, in both physiological and dopamine-depleted conditions (ξ=−0.4 and ξ=−0.8) (Fig. 5(b)).
As we compared the results to the physiological case, which is in line with experimental values,55 we found that the addition of dopamine depletion led to a decline in performance, which worsened as the depletion progressed (%CR decrease at the last trial set of 30 (20)% from physiological to mild parkinsonism states and of 40 (20)% to severe states, N=5).
4. Discussion
This study sets the computational basis of abnormal multiarea interactions in parkinsonism bringing the cerebellum8,9,10,12 to the forefront.
Incorporating the cerebellum into the closed-loop multiarea circuit provides compelling evidence showcasing how dopamine-dependent cerebellar dysfunction intensifies beta oscillations and hampers motor learning. This finding highlights the need to extend the pathophysiology of parkinsonism symptoms to multiple brain regions beyond the BG, both in experimental and computational models, with the cerebellum acting as a key player.
The multiscale approach adopted here required the integration of multiple SNNs and neural masses. The multiarea model passed a rigorous validation process. Indeed, it successfully replicated the activity of existing cerebellar and BG models,33,34 which were previously studied in isolation and validated against in vivo data. We deem this validation of the highest relevance to reliably capture the interactions among multiple brain regions acting in closed loop, generating de facto an innovative computational approach to the investigation of multiple brain circuit interactions.11,21
By challenging the multiarea model in both physiological and Parkinsonian conditions, we explored the physiology of the cerebellum — BG interactions.26,27 Following incorporation of dopamine-dependent dysfunction in the cerebellum,20 as well as in the BG,34 the simulations yielded results consistent with experimental observations Table 2, suggesting a possible direct cerebellum’s involvement in PD-related dynamics. The internal degeneration of the cerebellar cortex (i.e. PC apoptosis) impacted the beta oscillations uncovering a pronounced low-frequency peak in the β-band, as observed in experimental studies.60,64,65 Additionally, the simulations yielded a decrease in the θ-band (i.e. the tremor frequencies) in the cerebellum and thalamocortical loop which have been observed in experimental studies66,67 in PD with freezing of gait. These simulations thus identify the cerebellum as a core mechanism for the reinforcement of aberrant neural activity through the cerebello-thalamocortical loop in PD.31
Taking our investigation a step further, we delved into functional motor learning by simulating a virtual EBCC task,48 selected for it being simple in replication with respect to more complex motor tasks (as done in Zahra et al.68) but still suitable to assess the ability of the cerebellum to learn temporal associations. Remarkably, despite the altered cellular structure, the cerebellum demonstrated an adaptive capacity, albeit with reduced efficacy compared to the physiological state. This finding highlights the cerebellum’s ability to partially compensate for dopamine-dependent changes27 and underscores its importance in motor learning and adaptation processes.69
4.1. Comparison with similar models
It is worth noting that the proposed implementation does not represent the only multiarea, multiscale model investigating PD or the interactions between BG and cerebellum during motor learning.
The study by Meier et al.70 presents a multiscale model comprising spiking BG and thalamocortical mean-field areas implemented using TVB framework43 to investigate the network effects of deep brain stimulation (DBS) on the STN. The resulting model generates biologically plausible activity in resting state and during virtual DBS, resulting in a promising approach that could be developed as a clinical platform for neurosurgeons and used to design therapies for individual patients before surgical interventions.
Another example that aimed to explain pathological changes in the cortico-BG-thalamocortical is presented by Caiola and Holmes,71 where the authors create a multiarea firing rate model, designed for physiological realism without sacrificing analytical methods, and elucidate how altered connection strengths drive changes in firing rates observed in recordings, contributing to PD’s trademark beta oscillations.
Other interesting proposals have been recently presented by Baladron et al.,72 as well as in the work by Pimentel et al.,73 where the authors developed a systems-level computational model of motor learning, including a cortex-BG motor loop, the cerebellum, and central pattern generators representing the brainstem. The model can learn arm movements toward different motor goals and reproduce human data in a motor adaptation task with cognitive control, sharing our findings regarding the fundamental importance of building models that account for the interplay between BG and cerebellum.
Although all these studies represent essential milestones towards a better understanding of both PD and motor learning, they differ from our model in some crucial aspects. Despite the network in Meier et al.70 is composed of multiple cortical nodes leveraging the “TVB” framework, it does not model the cerebellar contribution explicitly, nor investigates functional motor learning impairments in parkinsonism. Similarly, Caiola and Holmes71 does not take into account the cerebellar contribution. The works by Baladron et al.72 and Pimentel et al.,73 on the other hand, provide a precise functional interpretation of the BG-cerebellum interplay and their model can produce complex motor responses that are close to human motor adaptation data. Still, their system-level design abstracts remarkably from the brain regions it represents and the authors do not consider any pathological scenario. With this being said, integrating the salient aspects of these two models with our network in a holistic representation would surely improve the descriptive (and possibly predictive) power of the proposed model.
Finally, it is worthwhile to compare the various methods employed in utilizing bioinspired models. In our approach, our goal was to construct a brain model capable of reproducing key physiological processes. This model serves to test additional hypotheses and simulate brain activity across various scales. An alternative method, which we didn’t adopt, involves implementing biologically plausible SNNs to emulate the computational capabilities of the brain. These SNNs can then be utilized as Artificial Neural Networks, typically applied to medical data for classification or regression problems such as intracranial electroencephalography recordings from epileptic patients for seizure detection or data from PD patients, as demonstrated in prior studies.74,75,76,77,78,79
4.2. Limitations and future developments
Although the results are satisfactory, the proposed model has some limitations that shall be addressed with further refinements aimed at improving its biological plausibility. First, not all the interactions between BG and cerebellum have been modelled. Specifically, the cerebellum sends di-synaptic inputs to the putamen through the thalamus, while outputs from the STN reach the cerebellar cortex through the pontine nuclei. However, there are no cues about the functional role of these connections,21 so their use in the models would require extensive research and careful hypotheses. Furthermore, certain additional connections have been neglected, such as the thalamic input to the striatum,80 which could be integrated into a more comprehensive version of the model.
Furthermore, no dopaminergic effects other than the PCs apoptosis were considered when simulating the functional motor task, and only the cerebellum was equipped with synaptic plasticity. Thus, in order to fully untangle the interplay between the BG and the cerebellum in motor processing, the dopamine-based reward signals in both the BG81 and in the cerebellum,16,82 should be introduced in the spiking model and varied according to the severity of the simulated Parkinsonian conditions.
The thalamocortical areas have been modeled using a highly simplified approach reducing the computational cost. Deploying the present model on dedicated hardware would allow converting these structures into detailed spiking models. These, in turn, could be used to investigate further the cerebellar impact on the oscillatory drive exerted by BG on the thalamocortical circuit in PD patients. In light of this, the present simulator could be adapted to run in the TVB framework.43
Lastly, since the outcome of the simulations could only be partially compared to experimental findings due to lack of data, the model is highly predictive in nature: in order to fully validate it, specific experiments shall be conducted to compare the model outcomes to signals obtained in vivo, although acquiring robust neural activity data from the same subject during the progression of the disease is a challenging task.
5. Conclusion
We developed a multiscale, multiarea model to investigate the role of the cerebellum in parkinsonisms. We found that our model highlights the importance of considering region and the effects dopamine depletion has on it in experimental and computational studies aimed at investigating parkinsonism. Furthermore, it represents an improvement over previous models that only reproduced a single area,83,34 using oversimplified mass models35 and did not explicitly model the cerebellum.84 Our approach paves the way for a unified physiopathological framework explaining Parkinsonian brain activity quantitatively across complexity scales.
Funding
The project “EBRAINS-Italy (European Brain ReseArch INfrastructureS-Italy),” granted by the Italian National Recovery and Resilience Plan (NRRP), M4C2, funded by the European Union –NextGenerationEU (Project IR0000011, CUP B51E22000150006, “EBRAINS-Italy”) to AA, AP, ED, and AM funded this work and fully covered the publication fees of this article.
Acknowledgments
The work of AA, AP, ED, and BG in this research is also supported by Horizon Europe Program for Research and Innovation under the Grant Agreement No. 101147319 (EBRAINS 2.0).
FJS is a PhD student enrolled in the National PhD in Artificial Intelligence, XXXVII cycle, course on Health and life sciences, organized by Universitá Campus Bio-Medico di Roma, supported by a Voucher (CEoI 4- Rodent microcircuits: RisingNet Whole-bRaIn rodent SpikING neural NETworks) from the European Union's Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreement No. 945539 (Human Brain Project SGA3).
The work of ED and AM in this research is also supported by the Italian Ministry of Research through the PNRR projects funded by the European Union – NextGenerationEU “A multiscale integrated approach to the study of the nervous system in health and disease” (Project PE0000012, CUP F13C2200124007, “MNESYS”).
Code Availability
The code used for this study can be freely accessed via the following Zenodo repository: https://zenodo.org/doi/10.5281/zenodo.10970202.
A. Spectral Variation with Dopamine Depletion in Cerebellum
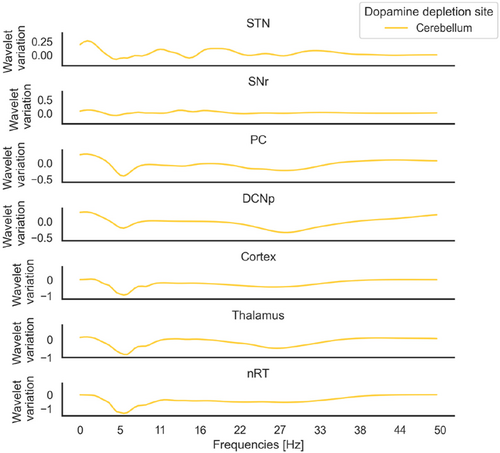
Fig. A.1. Spectral variation with dopamine depletion in cerebellum: spectrum values of the three mass models (cortex, thalamus, nRT), the STN, SNr and PC and DCNp. Each curve represents the variation of the power spectrum evaluated at the most severe case (depletion level −0.8) with respect to the physiological condition (ΔWT=WT pathological−WT physiologicalWT physiological).
B. Circular Variance of Mass Models’ Activities
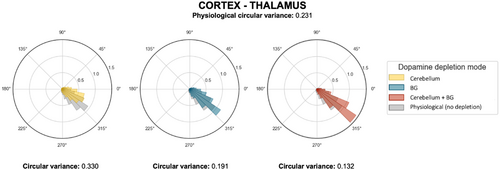
Fig. B.1. Circular variance of mass models’ activities: polar histograms of the phase differences between mass models’ activities and the corresponding circular variance values in three different sites of dopamine depletion (cerebellum, BG, and cerebellum + BG, with depletion level ξ=−0.8 and in physiological conditions).
C. Learning Protocol
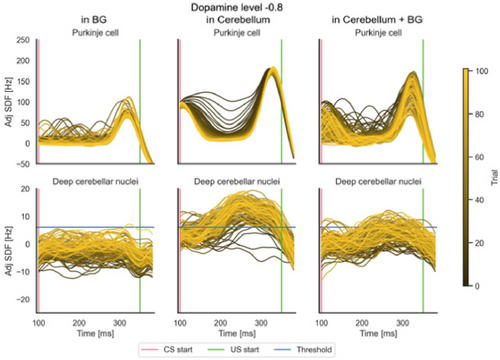
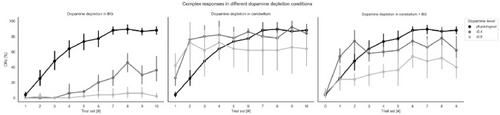
Fig. C.1. Learning protocol: EBCC results both in terms of activities of the main populations of interest (PCs and DCNp) and in terms of %CR. Panel (a) shows the results of the EBCC protocol when dopamine depletion is modeled in different sites (only BG on the left, only cerebellum in the center, cerebellum + BG on the right) at the most severe case (depletion level −0.8). The entire CS window is shown, with all trials overlaid (each curve represents the SDF within a single trial, and trials’ progression is shown with a shaded color). The signals are adjusted for the baseline evaluated in the 200 ms following the stimuli. US start and threshold for identification of CR are reported. In panel (b), the percentage of CR identified in each 10-trial block, at different sites (as in panel (a)) and magnitudes of dopamine depletion (0 = physiological state, −0.4, −0.8) are overlaid.
ORCID
Benedetta Gambosi  https://orcid.org/0009-0003-0816-8211
https://orcid.org/0009-0003-0816-8211
Francesco Jamal Sheiban  https://orcid.org/0000-0002-2297-0222
https://orcid.org/0000-0002-2297-0222
Marco Biasizzo  https://orcid.org/0000-0002-8988-5874
https://orcid.org/0000-0002-8988-5874
Alberto Antonietti  https://orcid.org/0000-0003-0388-6321
https://orcid.org/0000-0003-0388-6321
Egidio D’angelo  https://orcid.org/0000-0002-6007-7187
https://orcid.org/0000-0002-6007-7187
Alberto Mazzoni  https://orcid.org/0000-0002-9632-1831
https://orcid.org/0000-0002-9632-1831
Alessandra Pedrocchi  https://orcid.org/0000-0001-9957-2786
https://orcid.org/0000-0001-9957-2786
| Remember to check out the Most Cited Articles! |
|---|
|
Check out our titles in neural networks today! |


