Dynamical properties, modulation instability analysis and chaotic behaviors to the nonlinear coupled Schrödinger equation in fiber Bragg gratings
Abstract
The nonlinear coupled Schrödinger equation in fiber Bragg gratings is studied in this paper. The existence of soliton solutions and periodic solutions are proved by qualitative analysis, and exact solutions are given, as well as the parameter condition of each solution is described. Then the modulation instability (MI) analysis is carried out and the linear stability criterion is given. In particular, external perturbation terms are introduced to prove that the equation exists chaotic behaviors.
1. Introduction
In the real world, there are many models using data1,2,3,4,5,6 for model analysis. However, general mathematical models are always necessary due to this aspect. Some mathematical models are used to get some more general results. The nonlinear partial differential equations model (NPDE) is a very important model that can be used to analyze problems in a common sense. NPDE can be used to describe nonlinear physical phenomena, such as mathematics,7 engineering,8 electrical science9 and others. There are many NPDEs that have been extensively studied, such as generalized (2+1)-dimensional shallow water wave equation,10 the (3+1)-dimensional Burger system (3DBS) equation,11 Schrödinger equation12,13,14 and so many others.15,16 In this paper, we consider the nonlinear coupled Schrödinger equation in fiber Bragg gratings as17
Fiber Bragg grating has a large group velocity dispersion, by selecting characteristics such as frequency and nonlinearity of gratings, it can be applied in many fields, such as filter design18,19 and pulse compression technology20 and fiber Bragg grating can form optical solitons in a very short distance, and optical soliton plays an important role in the field of fiber optical communications.21,22 In particular, Eqs. (1) and (2) are a dual extension to the Kerr type of nonlinearity and are occasionally referred to as cubic–quintic–septic nonlinear form, having an important application in compensation for the dispersion velocity of one of the two sources of stable soliton transport over intercontinental distances.17 As a result, this equation has attracted the attention of many researchers in recent years. Zayed studied the nonlinear polynomial law and obtained the bright and singular soliton solution of the equation.17 Kamel constructed periodic and solitary wave solutions to this equation, representing the propagation of different waveforms in fiber Bragg gratings.23 The propagation of Bragg solitons is shown by studying the nonlinear pulse propagation of out-of-band frequency through Bragg grating when the grating is transmitted but highly dispersive.24 However, they didn’t conduct the qualitative analysis, and didn’t find all the traveling wave solutions.
Many famous methods are used to deal with NDPE, such as Darboux transform,25 sinh-Gordon equation expansion method,26 Bäcklund transformation,27 tanh method28 and the complete discrimination system for polynomial method (CDSPM),29,30,31,32 Among the above method, CDSPM is widely used,33,34,35 not only can it obtain the traveling wave solutions of many important NPDE, but it also can prove the existence of periodic and soliton solutions by qualitative analysis of equations. Kai uses this method to prove the existence of periodic soliton of Degasperis–Procesi model and Kudryashov equation.36,37 Hu uses this method for qualitative analysis of a generalized Kudryashov equation.38 Therefore, in this paper, this method is used to qualitatively analyze the equation to give the dynamical properties, proving that periodic solutions and soliton solutions exist, and construct all traveling wave solutions to verify it. In particular, the modulation instability (MI) of Eqs. (1) and (2) is analyzed, and the chaotic behaviors of the equation are observed by introducing perturbation terms.
2. Integral Form of Eqs. (1) and (2)
By taking the following transformation
When
3. Dynamical Properties of Eq. (15)
Dynamical system of (15) is as follows :
Case 1.N4=0, N3>0, N2>0, then F′(ϕ) is given by
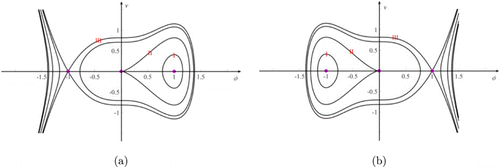
Fig. 1. (Color online) Dynamic system (16): (a) f5=−1, h2=−1, h1=−1, h0=0; (b) f5=1, h2=1, h1=0, h0=1.
Trajectory I implies that periodic solutions exist. Trajectories II and III indicate that bell-shaped soliton solutions exist.41
Case 2.N4=0, N3=0, N2>0, E2=0, we have
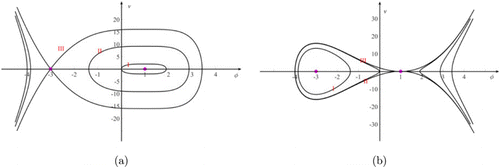
Fig. 2. (Color online) Dynamic system (16): (a) f5=−1, h2=−6, h1=8, h0=−3; (b) f5=1, h2=6, h1=−8, h0=3.
The trajectories I and II in Fig. 2(a) imply that the periodic solutions exist, the trajectory III indicates that the soliton solutions exist. However, in Fig. 2(b) trajectory I implies that the periodic solutions exist, and trajectories II and III imply that the bell-shaped soliton solutions exist.
Case 3.N1>0, N2>0, N3>0, we can get
The specific phase portrait is shown in Fig. 3, Trajectories I and III imply that periodic solutions exist, and trajectories II and IIII indicate that bell-shaped soliton solutions exist.
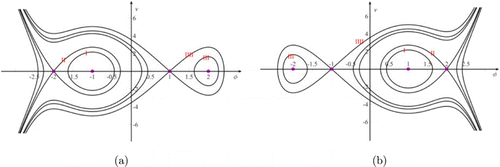
Fig. 3. (Color online) Dynamic system (16): (a) f5=−1, h2=−5, h1=0, h0=4; (b) f5=1, h2=5, h1=0, h0=−4.
Case 4.N4<0, N3N2≥0, we can get
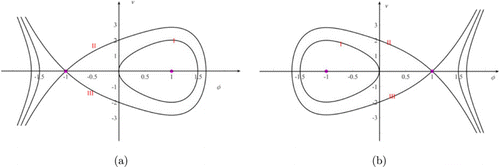
Fig. 4. (Color online) Dynamic system (16): (a) f5=−1, h2=0, h1=0, h0=−1; (b) f5=1, h2=0, h1=0, h0=1.
Trajectory I implies that periodic solution exists. Trajectories II and III imply that soliton solution exists.
Here are other five cases where there are no soliton solutions and periodic solutions, it does not help our discussion, we omit specific discussion.
4. Exact Solutions of Eq. (15)
Transform (15) as
(I) When N5=0, N4=0, N3>0, E2≠0, we can get
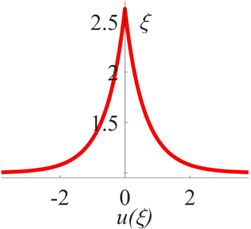
Fig. 5. (Color online) Peakon bright soliton solution when k3=−2, k2=0, k1=0, k0=1.
(II) When N5=0N4=0N3=0, N2≠0, F2≠0, we can get
(III) When N5=0, N4=0, N3=0 and N2≠0, F=0
(IV) When N5=0, N4=0, N3=0, N2=0, F(τ) is given by could be shown as
(V) When N5=0, N4=0, N3<0, E2≠0, we have
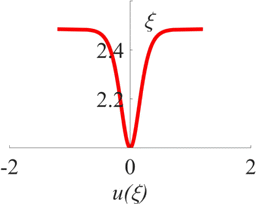
Fig. 6. (Color online) Dark soliton solution when k3=0, k2=−5, k1=415, k0=−92.
(VI) When N5=0 and N4>0, we get
(VII) When N5=0, N4=0, N3<0, we have
(VIII) When N5>0, N4>0, N3>0, N2>0 we obtain
(IX) When N5=0, N4=0, N3>0, E2=0, we obtain
(X) When N5=0, N4<0, we get
(XI) When N5>0, N4≤0, N3≤0, N2≤0, we have
(XII) When N5<0, we have
5. Stability Analysis
MI analysis is of great significance for nonlinear equations42,43,44,45. In this section, due to ϕ2(ξ)=Πϕ1(ξ), we can get
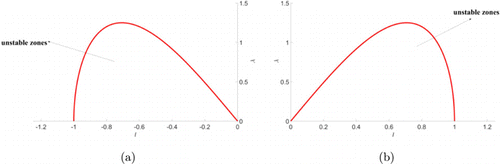
Fig. 7. (Color online) MI zones when , , ,
In this case the MI gains spectrum , which can be expressed as
6. Chaotic Studies of Eq. (15)
Chaotic phenomena can be used to describe many complex physical phenomena, such as analysis of neural network and optical fiber communications.48,49 Therefore, we study the chaotic phenomena of the equation. We add the perturbed term to the dynamic system (15) to get the following perturbed system :
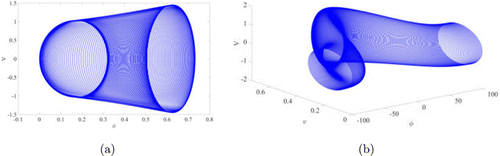
Fig. 8. (Color online) The phase graph of the perturbed system with Gaussian distribution when , , ,
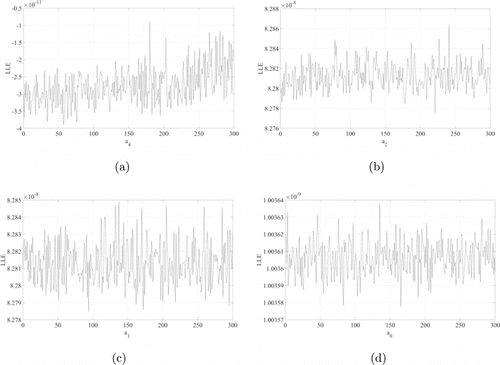
Fig. 9. (Color online) The perturbed system (15): (a) LLE for ; (b) LLE for ; (c) LLE for ; (d) LLE for .
We study another perturbation function: the cosine function. If , , , , , . The corresponding phase diagram in Fig. 10 and the relationship between LLE and parameters are shown in Figs. 11(a)–11(d). The analysis of LLE is similar to the Gaussian perturbation, it is clear that the parameters , , and have effects on chaotic behaviors of the perturbed system. It is easy to find that there is chaotic behaviors in this case and that the solution is not unique, and the phase portraits are different from the Gaussian perturbation, which confirms the above conclusion. The chaotic behaviors to this equation may have many potential physical applications which can provide a new direction for future study.
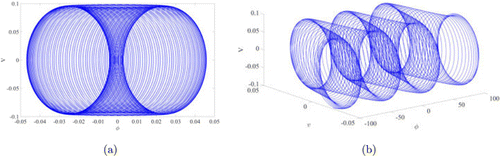
Fig. 10. (Color online) The phase graph of the perturbed system with Gaussian distribution when , , , , .
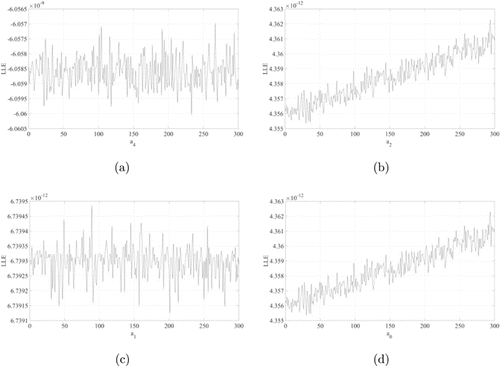
Fig. 11. (Color online) The perturbed system (15): (a) The LLE for ; (b) The LLE for ; (c) The LLE for ; (d) The LLE for .
7. Conclusion
The purpose of this study is to solve the nonlinear coupled Schrödinger equation in fiber Bragg gratings by CDSPM. The method used in this paper is simple but effective. We can obtain the existence of solitons and periodic solutions by qualitative analysis through its dynamical system without constructing the exact solutions. We also give concrete solutions to verify our solutions by conducting the quantitative analysis and all traveling wave solutions are given, and some new solutions of the equation are shown, namely the rational type solution, elliptic function solutions, which makes our results more complete. In particular, the MI of the original equation is analyzed. The linear stability is presented, and the critical condition for stability is provided. Finally, the chaotic behaviors of the equation under different perturbation terms are shown. As far as we know, these findings to this equation are given first and a new research direction for the equation is provided.



