Mean-reverting diffusion model-enhanced acoustic-resolution photoacoustic microscopy for resolution enhancement: Toward optical resolution
Abstract
Acoustic-resolution photoacoustic microscopy (AR-PAM) suffers from degraded lateral resolution due to acoustic diffraction. Here, a resolution enhancement strategy for AR-PAM via a mean-reverting diffusion model was proposed to achieve the transition from acoustic resolution to optical resolution. By modeling the degradation process from high-resolution image to low-resolution AR-PAM image with stable Gaussian noise (i.e., mean state), a mean-reverting diffusion model is trained to learn prior information of the data distribution. Then the learned prior is employed to generate a high-resolution image from the AR-PAM image by iteratively sampling the noisy state. The performance of the proposed method was validated utilizing the simulated and in vivo experimental data under varying lateral resolutions and noise levels. The results show that an over 3.6-fold enhancement in lateral resolution was achieved. The image quality can be effectively improved, with a notable enhancement of ∼66% in PSNR and ∼480% in SSIM for in vivo data.
1. Introduction
Photoacoustic microscopy (PAM) represents a promising imaging modality combining the high- spatial resolution of optical imaging with the profound tissue penetration capability of ultrasound imaging.1 Capitalizing on these advantages, PAM has garnered substantial attention in biomedical research over recent decades,2,3,4 exhibiting extensive preclinical and clinical applications in realms such as tumor detection,5 dermatology,6 and vascular morphology assessment.7 Diverging according to imaging modality, PAM can be delineated into optical-resolution photoacoustic microscopy (OR-PAM)8 and acoustic-resolution photoacoustic microscopy (AR-PAM).9 OR-PAM harnesses optical detection methodologies, achieving remarkable lateral resolution (<5μm)10 and commendable imaging quality. However, light scattering within biological tissues limits the penetration depth of OR-PAM (at most ∼1–2mm). In contrast, owing to its acoustic properties, AR-PAM demonstrates a superior capability for deeper penetration into biological tissue structures (∼3–10mm).11 Nevertheless, this enhanced effectiveness comes with a reduction in lateral resolution (>50μm) and an accompanying increase in background noise, thereby adversely affecting the image contrast and overall quality. Realizing an AR-PAM imaging system endowed with superior lateral resolution without compromising imaging depth and fidelity would significantly propel the advancement and application of PAM systems.
Enhancing the lateral resolution in AR-PAM holds promise for applications such as photoacoustic velocimetry12 and in vivo disease characterization.13 In PAM, the fusion of high lateral resolution and deep penetration is crucial for further realizing more medically valuable imaging applications. Research has delved into the prospect of integrating OR-PAM and AR-PAM at the system level. For instance, Xing et al. proposed an integrated optical-resolution and acoustic-resolution PAM system by utilizing distinct channels of optical fiber bundles for light transmission.14 Jiang et al. achieved a PAM system covering a range from optical to acoustic resolution by generating adjustable-size focused laser spots at the tip of fiber bundles using a zoom lens.15 In another study, Song et al. introduced a single-pixel imaging strategy,16 enabling multiscale imaging by adjusting the spatial frequency of stripes without relying on conventional mechanical scanning. This approach allows for lateral resolution adjustment within a range from micrometers to tens of micrometers. However, despite effectively combining the high resolution of OR-PAM with the deep tissue penetration advantage of AR-PAM, these methods rely on costly physical equipment, which limits their widespread application to some extent. An alternative viable strategy involves overcoming this challenge through computational methods combined with data-driven approaches. By further studying and understanding the correlations between OR-AR PAM datasets, particularly the characteristics of acoustic-resolution photoacoustic signals at specific depths, establishing a mapping relationship between the two datasets would render achieving high lateral resolution in AR-PAM practically feasible. This could potentially offer a new avenue for enhanced imaging of tissue morphology in deeper regions.
In recent years, deep learning technology, endowed with potent feature extraction and learning capabilities, has been extensively employed in biomedical image processing,17,18,19,20 including the enhancement of quality and resolution in PAM images. Sharma and Pramanik applied convolutional neural networks (CNNs) to augment the defocused resolution in AR-PAM images.21 Zhang et al., leveraging a fusion of deep CNN priors and model-based methods,22 successfully realized an adaptive enhancement technique within a unified framework for AR-PAM imaging. However, CNNs trained with pixel-level loss typically focus solely on overall pixel disparities, often failing to effectively capture detailed image information, thereby resulting in excessively smoothed network outputs.23 Wang et al. proposed a strategy based on a fully dense U-Net (FDU-Net) for signal enhancement in the defocused regions and enhancement of spatial resolution in OR-PAM,24 overcoming the shallow depth of field challenge faced by OR-PAM. Sharma and Pramanik obtained high-resolution AR-PAM images without noise via FDU-Net.25 Despite the advancements achieved by FDU-Net in enhancing PAM image quality and resolution, research indicates that it could still face issues like overfitting or computational overhead, especially when dealing with complex scenes.
With the rapid advancement of deep learning, numerous generative models, including generative adversarial network (GAN),26 variational autoencoder (VAE),27,28 denoising diffusion probabilistic model (DDPM),29 and score-based generative model,30 have demonstrated notable superiority and vast potential in the realm of image processing and reconstruction. Compared to GANs, diffusion models exhibit heightened precision in aligning with the distributions of real images, bolstering their robust adaptability to diverse input conditions and broad applicability across varied datasets. Additionally, diffusion models show significant improvements in stability, effectively obviating the issue of mode collapse during training. Particularly noteworthy is the diffusion model proposed by Song et al., based on stochastic differential equation (SDE),31 which embodies formidable generative capability, facilitating the generation of high-quality samples, thereby offering significant assistance in medical image reconstruction, artifact removal, and image synthesis.32,33,34 The SDE-based diffusion model progressively introduces Gaussian noise into the image during the forward process until the signal is entirely submerged. In the reverse process, it simulates a reverse-time SDE, commencing sampling from pure noise to restore high-quality images. However, traditional diffusion models entail extensive iterative computations to achieve high-quality image generation or reconstruction, thereby augmenting computational resource requirements and time expenditures. Inspired by this, the present study proposes a strategy for enhancing the resolution of the AR-PAM images and denoising based on the mean-reverting diffusion model.35 The original high-quality image is diffused solely to a mean state with fixed Gaussian noise, obviating the necessity for introducing pure noise. Simulated point data and in vivo mouse experimental data are utilized to evaluate the performance of the proposed method. The results demonstrate significant enhancement in the resolution of the AR-PAM images and effective denoising. Through the adoption of the proposed approach, it is feasible to achieve significantly higher-resolution imaging in terms of lateral resolution surpassing traditional AR-PAM imaging techniques. This holds pivotal significance in addressing the trade-off between penetration depth and lateral resolution in OR-PAM and AR-PAM.
2. Materials and Methods
2.1. Dataset acquisition
In deep learning tasks, large-scale, and high-quality datasets are crucial for optimizing the performance of network models. However, for the task of enhancing the resolution of the AR-PAM images to OR-PAM images, acquiring a substantial number of in vivo AR-OR PAM image pairs for training presents significant challenges. By adopting the numerical methods proposed below, it is possible to ensure the performance of the network model even in the face of limited in vivo OR-PAM imaging data.
The training data required for the experiment consist of high-resolution OR-PAM images paired with corresponding low-resolution AR-PAM images. The OR-PAM dataset,36 provided by the Photoacoustic Imaging Laboratory of Duke University and publicly available, includes a total of 381 maximum amplitude projection OR-PAM images of varying sizes. These images primarily comprise in vivo capillary images of mouse brains, with a few images of mouse ears and tumors. The OR-PAM images obtained experimentally inevitably contain noise and isolated bright spots. Thus, a series of preprocessing methods, including threshold cropping, median filtering, Gaussian filtering, and adaptive histogram equalization, are employed to eliminate extreme brightness and enhance the vascular structure features within the images, thereby improving the quality of the existing dataset. Additionally, the processed images are flipped and rotated by ±30∘ along different orientations (horizontal, vertical, and diagonal) to simulate vascular structures with various spatial distributions. Due to the large size of the original dataset images and to match the input size (256×256) of the model, the images are randomly cropped, significantly increasing the amount of training data. These techniques aim to artificially expand the distribution of PAM data used for training, enabling the network to exhibit robustness and good generalization capabilities.
Through the aforementioned processes, a substantial quantity of high-quality OR-PAM images can be obtained, yet there is a shortage of corresponding AR-PAM images. Consequently, this study employs a numerical method to simulate the degradation process from OR-PAM to AR-PAM, thereby acquiring the paired AR-OR PAM images. In principle, it is assumed that the AR-PAM system operates as a linear space-invariant system around the focus area,37 as shown in the following equation :
Then, the PSF kernel can be generated using Eq. (3), and specific AR-PAM images with the given FWHM can be obtained through Eq. (1). To verify the adaptability of the proposed method, the FWHM of the simulated AR-PAM images is set to 35, 55, 75, and 95μm for the experiment. Figures 1(a)–1(e) show the simulated AR-PAM images for these conditions alongside the corresponding original OR-PAM image, where the simulated images have the signal-to-noise ratio (SNR) of 35 dB. As the FWHM increases, vascular outlines become blurred, and both the lateral resolution and contrast of the images decrease, with some capillary structures becoming indistinguishable (as shown by the white arrows in Figs. 1(a)–1(d)). Additionally, considering that real photoacoustic images always contain noise, varying levels of Gaussian noise (represented by n in Eq. (1)) are added to the low-resolution images to simulate different degrees of noise disturbance, thereby testing the robustness of the proposed model. The noise of specified magnitude is introduced into the images utilizing the addNoise function provided by the k-Wave MATLAB toolbox.38 As shown in Figs. 1(g)–1(i), the SNR starts at 35 dB and gradually decreases to 15 dB in 10 dB steps. Meanwhile, the AR-PAM image without noise is preserved (Fig. 1(f)) for further comparison. Figure 1(j) shows the corresponding OR-PAM image. The FWHM in Figs. 1(f)–1(i) is all set to the typical value of 55μm for the AR-PAM system. As indicated by the white arrow in Fig. 1(g), when the SNR is at 35 dB, the impact of noise in the AR-PAM image is relatively mild. However, as the SNR decreases, the faint signals indicated by the arrows in Figs. 1(h) and 1(i) are gradually overwhelmed by noise, making capturing and analyzing vascular structural features challenging.

Fig. 1. Datasets for deep learning. (a)–(d) are simulated AR-PAM images of the blood vessel with the FWHM of 35, 55, 75, and 95μm, respectively. (e) is the corresponding OR-PAM image. (f) is the AR-PAM image of the blood vessel without noise. (g)–(i) are AR-PAM images with the SNR of 35, 25, and 15 dB, respectively. The FWHM of (f)–(i) is set to 55μm. (j) is the corresponding OR-PAM image. (k) is the simulated AR-PAM image of the point data without noise. (l)–(n) are the simulated AR-PAM images with SNR of 35, 25, and 15dB, respectively. (o) is the corresponding ground truth. The FWHM of (k)–(n) is set to 55μm. GT, ground truth; NPA, normalized photoacoustic amplitude; FWHM, full width at half maximum; SNR, signal-to-noise ratio.
Additionally, point simulation dataset is also employed to estimate the limit of lateral resolution achieved by the model. For each image of the point data, an empty 256×256 matrix is initially created with all elements set to zero. Subsequently, one to nine sets of random points are generated per image, with the position and orientation (horizontal or vertical) of each set of points being determined randomly. The spacing between each set of points is also randomly assigned. Based on these random parameters, the pixel values at the designated positions in the image matrix are set to 255, thereby generating a variety of simulated point images with different configurations to form a comprehensive dataset. The dataset with random spacings and positions is utilized for training, and the dataset with predefined spacings and positions is utilized for testing to estimate the limits of lateral resolution achievable by the proposed method. The lateral resolution of all images is set to 55μm. The simulated AR-PAM image without noise is shown in Fig. 1(k). The addNoise function provided by the k-Wave MATLAB toolbox is employed to introduce three distinct noise levels into the AR-PAM images, resulting in SNR of 35, 25, and 15 dB, respectively, as shown in Figs. 1(l)–1(n). Figure 1(o) shows the corresponding ground truth.
2.2. Principle of lateral resolution enhancement based on diffusion model
2.2.1. Mean-reverting diffusion model
To enhance AR-PAM images, this study employs a diffusion model based on mean-reverting SDE. This model transforms a high-quality image into a degraded version, characterized as a mean state with fixed Gaussian noise. The original high-quality images are then recovered by simulating the corresponding reverse-time SDE. The idea of using SDEs to model the diffusion process in diffusion models was initially proposed by Song et al.31 By continuously adding noise to the data distribution in the forward SDE, a pure noise prior to close to the Gaussian distribution is obtained. In the reverse process, the prior distribution is transformed back into the corresponding data distribution by continuous denoising, achieving the purpose of generating samples from noise. Compared to the traditional diffusion models, the SDE-based diffusion model can model the entire diffusion process in the continuous time domain, which allows for more precise control over the dynamics of the generation process. Furthermore, since the SDE simulates the natural diffusion processes (such as the Brownian motion), it generates samples with smoother transitions and better detail fidelity. Assuming {xt}Tt=0 is a continuous diffusion process, where xt∈Rd, t∈[0,T]. p0 represents the initial data distribution, and pT represents the prior distribution. If x0∈Rd is the initial condition, then the forward process can be described by the following equation :
However, using traditional SDEs to model the diffusion process requires transforming the original data distribution into a pure noise prior distribution. This often demands more iterations and computational resources to obtain high-quality samples. Building on this, Luo et al. proposed image restoration with mean-reverting SDE (IR-SDE),35 which introduces the parameter μ in the original model to directly model the diffusion process from the high-quality image x0 to its degraded counterpart μ. Therefore, Eq. (4) can be reformulated as
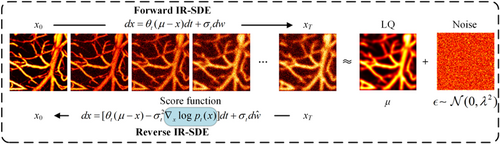
Fig. 2. Overview of the mean-reverting SDE structure. LQ, low-quality.
However, in scenarios of complex degradation, directly learning the instantaneous noise within a specified time period presents challenges. Consequently, an approach grounded in a maximum likelihood objective is adopted. For a specified x0, stability in the training process is attained, further enhancing the quality of image generation, by identifying the optimal path x1:T. The likelihood p(x1:T|x0) can be maximized, according to the following equation :
2.2.2. Lateral resolution enhancement of AR-PAM based on diffusion model
The degradation process from OR-PAM to AR-PAM (the mean state μ) is initially modeled in the framework of IR-SDE. Subsequently, by simulating the reverse SDE, the mean state is restored to a high-quality image. During the training phase, as shown in the upper part of Fig. 3(a), AR-OR PAM image pairs are fed into the network to solve the sole uncertain factor in Eq. (9): the score function ∇xlogpt(x). The network needs only the noise level ϵt at any given time from x0 to μ determine the score function of data distribution at specific moments. Here, an enhanced nonlinear activation-free network (NAFNet)39 is adopted to replace U-net as the backbone network for noise prediction, with its simplified network architecture shown in Fig. 3(b). Notably, certain specifics have been intentionally left out for brevity, including downsampling and upsampling layers, feature fusion modules, input/output, etc. Compared to U-net, NAFNet achieves higher image restoration quality and computational efficiency while utilizing fewer model parameters. NAFNet embraces an innovative design concept known as nonlinear activation free, which eliminates all nonlinear activation functions. Instead of conventional activation functions, the network introduces “SimpleGate”, an element-wise operation that divides feature channels into two parts and multiplies them with each other to generate the output. This architectural approach decreases computational complexity while significantly enhancing network performance. To address the temporal embedding challenge, NAFNet has been optimized with the introduction of an improved nonlinear activation-free block (shown in Fig. 3(c)). Before the attention layer and feed-forward layer, an additional multi-layer perceptron (MLP) has been incorporated to generate channel-wise scaling and offset parameters (α and β). This enhancement not only reinforces the adaptability of the model to temporal dynamics but also provides finer control over the operations of attention and feedforward layers, thereby further enhancing the performance and flexibility of the model.

Fig. 3. The model flowchart and network architecture. (a) shows the flowchart encompassing both the training and reconstruction processes of the model. (b) shows the simplified architecture of the noise network in the U-net configuration. (c) shows the enhanced NAFBlock, a nonlinear activation-free block. PSF, point spread function; LQ, low-quality; HQ, high-quality; SCA, simplified channel attention; NAFNet, nonlinear activation free network; Conv, convolution; MLP, multi-layer perceptron; Layer Norm, layer normalization.
During the reconstruction phase (as shown in the lower part of Fig. 3(a)), noise embedded in the image is gradually removed by reverse simulating the diffusion path, effectively restoring a high-quality image from the intermediate mean state. Specifically, sampling begins with a noisy version μ+ϵ of the low-quality image and iteratively solving the reverse-time SDE using the Euler–Maruyama numerical method. The core principle of the Euler–Maruyama method involves dividing continuous time intervals into discrete small-time steps Δt. At each time step, the noise network ˜ϵϕ calculates the next image state xt−1 based on the predicted score function derived from the current image state xt and temporal information t, as shown in Eq. (9). It is noteworthy that the Euler–Maruyama method approximates the stochastic term σtΔˆw through an incremental form of the Wiener process, where Δˆw denotes the increment of the reverse-time Wiener process, typically simulated as √Δtz (where z is a standard normal random variable with mean 0 and variance 1). In backward simulation, selecting an appropriate time step is crucial, as it significantly influences the precision and stability of the approximation. Importantly, in the execution of revere-time SDE, the time step t progresses from T to 0, with the corresponding subscript t exhibiting a decreasing trend.
The network training adopted the Lion optimizer combined with cosine annealing learning rate scheduling, where the initial learning rate was set to 4×10−5. The maximum number of training iterations was set to 700,000. Model checkpoints were saved every 5000 iterations. The max noise level was fixed at 50, and the batch size was set to 2. Employing the simulation method described in Sec. 2.2, the dataset consisting of 5000 paired AR-OR PAM images was acquired. Both the blood vessel and point simulation dataset consisted of 4500 images for the training set (90%) and 500 images for the test set (10%). During the reconstruction phase, the iteration count was set to 100, and the input size was set to 256×256. The proposed method was implemented based on the PyTorch framework, primarily within a Python environment. In this study, computational tasks were executed on a graphical processing unit (GPU; GeForce RTX 3060Ti).
2.3. Baseline methods
The Richardson–Lucy Deconvolution,40,41 CycleGAN,42 FDU-Net24 are selected for comparison with our method in this study. RL method is grounded in the concept of maximum likelihood estimation and progressively optimizes the image restoration through multiple iterations. During each iteration, the algorithm updates the image based on the current restoration and the known system blur kernel (PSF). Upon reaching the specified convergence criteria, the iterations cease, yielding the final restored image considered an estimation of the clear image. Additionally, to reduce potential noise amplification and ringing artifacts introduced by RL deconvolution with the increasing iterations, several additional processing steps are implemented to enhance the quality of the restored images, ensuring minimal interference with metric evaluations.
CycleGAN is an unsupervised learning framework intended for image-to-image translation between two distinct domains. The defining characteristics of CycleGAN include the implementation of cycle consistency loss, which ensures the retention of essential features from the original image after translation, and its capability to function without the need for paired training data. This framework is particularly notable for its versatility and effectiveness in the task of image enhancement. FDU-Net is an advanced deep learning model based on the U-Net architecture, primarily employed in medical imaging, segmentation, and restoration tasks. While the basic U-Net model performs well for medical image segmentation, a more densely connected network is more suitable for the task of image prediction. To achieve this, FD blocks are incorporated into both the contraction and expansion paths of U-Net, densifying the network. These dense connections enhance information flow, avoid redundant feature learning, and reduce network parameters, which in turn lowers computational costs and accelerates image processing. Its outstanding performance has been validated in PAM images.24 Both of the CycleGAN and FDU-Net employed the same dataset as the proposed method for training and testing purposes. During the training phase, low-resolution AR-PAM images are fed into the network, while the paired OR-PAM images serve as the gold standard.
3. Results
3.1. Points simulation data
During the testing phase, simulations of points with varying noise levels and lateral spacing are used to assess the feasibility of the model, as shown in Fig. 4. Figure 4(a) presents the AR-PAM image without noise, while Figs. 4(b)–4(d) show images with SNR values of 35, 25, and 15 dB, respectively, all with the FWHM set to 55μm. Figures 4(e)–4(h) demonstrate the iterative process of the model for each of the four inputs shown in Figs. 4(a)–4(d). Figures 4(i)–4(l) represent the same ground truth (OR-PAM image). Reconstruction begins with the noisy version μ+ϵ of the low-quality image, and by the 25th iteration, the outlines of the points remained moderately blurred. With the advancement of iterations, noise within the images is gradually removed, significantly enhancing the clarity of the points. Ultimately, after the 100th iteration, all points in the input images under different levels of SNR are effectively reconstructed to yield output images highly resembling the ground truth.

Fig. 4. Results of resolution enhancement and denoising under different levels of SNR. (a) is the AR-PAM image without noise. (b)–(d) are the AR-PAM images with the SNR of 35, 25, and 15 dB, respectively. The FWHM of (a)–(d) is set to 55μm. (e)–(h) show the process of the reverse iteration, with the final column showing the output images. (i)–(l) show the same ground truth. (a1)–(d6) are the close-up images of the white dashed boxes 1–3. (e1)–(e3) show the same close-up images corresponding to the ground truth. (m)–(o) show the signal distribution along the white dashed lines 1–3 indicated in (a1)–(d6) under different levels of SNR, respectively. NPA, normalized photoacoustic amplitude; SNR, signal-to-noise ratio; In1, input image 1 without noise; In2, input image 2 with the SNR of 35 dB; In3, input image 3 with the SNR of 25 dB; In4, input image 4 with the SNR of 15 dB; GT, ground truth; Out1, output image 1 without noise; Out2, output image 2 with the SNR of 35 dB; Out3, output image 3 with the SNR of 25 dB; Out4, output image 4 with the SNR of 15 dB.
To further analyze the resolution limit of the enhanced images, the points with horizontal spacings of 70, 55, and 15μm are selected for analysis, as indicated by the white dashed boxes 1–3 in Figs. 4(a)–4(d), and the white arrows in the ground truth. Figures 4(a1)–4(d6) show the close-up images of the selected points from Figs. 4(a)–4(d) under different levels of SNR. Figures 4(e1)–4(e3) represent the corresponding ground truth. Figures 4(m)–4(o) represent the distribution of signal intensity at positions indicated by the white dashed lines in Figs. 4(a1), 4(a3), and 4(a5) under various levels of SNR. The points with a spacing of 70μm in the input image can be clearly distinguished (as shown in Fig. 4(m)), and those with a spacing of 55μm are on the threshold of being distinguishable (as shown in Fig. 4(n)), suggesting an estimated lateral resolution limit of ∼55μm for the input AR-PAM images. Nevertheless, for the points spaced 15μm apart, their separation is significantly below the resolution limit of the input image, resulting in overlapping signals that are indistinguishable (as shown in Fig. 4(o)). In contrast, in the enhanced results of the model, the points with spacings of 70, 55, and 15μm can all be effectively distinguished under different levels of SNR (as shown in Figs. 4(m)–4(o)), indicating that the lateral resolution of the enhanced images of the model exceeds 15μm. Furthermore, the positions and intensities of the points in the output images are highly consistent with the corresponding ground truth. These results suggest that the proposed method can significantly enhance the lateral resolution of the AR-PAM images under various levels of noise disturbance.
The mean and standard deviation of peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) are calculated based on 50 test images to quantitatively evaluate the performance of the model, as shown in Table 1. Under conditions without noise and with the SNR of 35 and 25 dB, respectively, the PSNR of the enhanced images surpasses 45 dB, exhibiting enhancements by ∼91%, 92%, and 102% in terms of dB values compared to their respective input images. As the SNR decreases stepwise from 35 dB to 15 dB at intervals of 10 dB, the SSIM of the output images, compared to the input images, improved by 0.68, 9.5, and 309 times, respectively. These results demonstrate that the proposed method effectively enhances the lateral resolution and image quality of the AR-PAM images across various SNR levels, even under extreme conditions such as the SNR of 15 dB.
| Input image | Output image | |||
|---|---|---|---|---|
| Noise level | PSNR/dB | SSIM | PSNR/dB | SSIM |
| Without noise | 23.88±2.23 | 0.93±0.038 | 45.71±2.52 | 0.93±0.002 |
| 35 dB | 23.68±2.13 | 0.56±0.023 | 45.55±3.18 | 0.94±0.002 |
| 25 dB | 22.30±1.57 | 0.09±0.004 | 45.13±3.56 | 0.95±0.002 |
| 15 dB | 16.81±0.51 | 0.003±0.001 | 38.33±2.97 | 0.93±0.007 |
3.2. In vivo experimental data
3.2.1. Comparison experiment
The performance of the proposed model is further evaluated using in vivo experimental data. Figures 5(a) and 5(b) show the iterative reconstruction process of AR-PAM images with SNR of 35 dB and FWHM of 55μm using the proposed method and RL deconvolution, respectively. For the results of RL deconvolution, at the 20th iteration, the image quality has improved, with some capillaries becoming distinguishable (as indicated by the three white arrows in Fig. 5(b)). However, with the increasing iterations, the improvements become less noticeable, and the final degree of image restoration is limited. For the proposed method, reconstruction starts from the low-quality noisy image. As shown in Fig. 5(a), noise is gradually removed from the 60th iteration onwards, and the outlines of blood vessels become clearer. When the iteration exceeds 80th, most capillaries emerge from the noise (as indicated by the three white arrows in Fig. 5(a)), significantly enhancing image clarity and contrast (more details about the iteration process are available in Visualization 1). Figures 5(c) and 5(d) quantitatively show the variations of PSNR and SSIM with iteration numbers. The RL deconvolution method slightly improves SSIM at the initial stage. However, with the increase in the number of iterations, SSIM tends to stabilize or even decline, and PSNR also shows a similar decreasing trend, both ultimately maintaining low values (PSNR tends toward 13.54 dB, SSIM tends toward 0.59). For the proposed method, PSNR and SSIM remain lower than those of the RL method in the initial iterations before the positions indicated by the red arrows in Figs. 5(c) and 5(d) due to the presence of considerable noise in the images. Nevertheless, as iterations progress beyond 80th iteration, noise in the images is gradually removed, leading to a rapid increase in PSNR and SSIM, significantly surpassing the results of RL deconvolution. At the 100th iteration, PSNR and SSIM reach 31.96 dB and 0.91, respectively. It should be noted that the two performance curves of the proposed method in Figs. 5(c) and 5(d) both rise very slowly at the beginning and is not fully stabilized in the last few iterations. This results from the inherent processing order of the two types of degradation of the model. Mean-reverting diffusion model tends to prioritize the primary degradation (i.e., deblurring) and only performs Gaussian denoising in the final few iterations, which is also noted in Ref. 35. As a result, the performance curves rise slowly in the early stages (the first 60 iterations). It can be observed in Fig. 5(a) that, during the iteratively reconstruction process of the blood vessels, most of the blurring is removed in the intermediate time steps (the first 60 iterations). However, due to the presence of Gaussian noise, the improvement in PSNR and SSIM is slow. In the final few iterations, the model begins to focus on denoising, which leads to a rapid improvement in image quality. This is reflected in the performance curves rising sharply and converging fully at the 100th iterations. In conclusion, these results demonstrate that the proposed method achieves significantly superior performance in enhancing the resolution of the AR-PAM image compared to the baseline.

Fig. 5. Reconstruction results of AR-PAM image with SNR of 35 dB and FWHM of 55μm under different methods. (a) and (b) show the results under different iterations using the proposed method and RL deconvolution method, respectively. (c) and (d) show the variation of PSNR and SSIM with iterations. (e) is the input image. (f)–(i) is the result of our proposed method, RL Deconv, CycleGAN and FDU-net respectively. (j) is the ground truth. GT, ground truth; NPA, normalized photoacoustic amplitude; RL Deconv, Richardson–Lucy deconvolution.
Figure 5(e) shows the input AR-PAM image under the condition with lateral resolution of 55μm and SNR of 35 dB. Figures 5(f)–5(i) show the enhancement results of AR-PAM using the proposed method, RL deconvolution, CycleGAN, and FDU-Net respectively. And the ground truth is shown in Fig. 5(j). RL deconvolution shows limited improvement in lateral resolution, with most areas remaining blurry. Both CycleGAN and FDU-Net enhance the lateral resolution of AR-PAM to some degree, but the loss of high-frequency information results in missing details and some discrepancies with the ground truth. The proposed method significantly enhances the lateral resolution and image quality of AR-PAM, preserving most details consistent with the ground truth. Quantitatively, our method increases PSNR and SSIM of AR-PAM to 31.96 dB and 0.91, respectively, which are 18.42 dB and 0.32 higher than RL deconvolution, 2.5 dB and 0.03 higher than CycleGAN, and 3.3 dB and 0.17 higher than FDU-Net. In conclusion, the proposed method not only effectively enhances lateral resolution and image quality but also retains most blood vessels’ details, achieving optimal image quality and enhancement performance consistent with the ground truth.
3.2.2. Results on different lateral resolutions
Given the variation in lateral resolution among different AR-PAM imaging systems, a series of experiments are designed to validate the adaptability and effectiveness of the proposed model to diverse inputs. AR-PAM images with the FWHM of 35, 55, 75, and 95μm are synthesized according to Eq. (1), covering the resolutions of most AR-PAM imaging systems. The SNR of all AR-PAM images is set to 35 dB to simulate noise in real imaging systems. Figures 6(a)–6(d) present the output results of the model when AR-PAM images with the FWHM of 35, 55, 75, and 95μm are used as inputs, respectively. Figures 6(e)–6(h) show the corresponding input images. As a reference, Figs. 6(i)–6(l) show the same ground truth (OR-PAM image). As the FWHM increases, the topological structure of the AR-PAM images gradually becomes blurred. The capillaries indicated by the two white arrows in Figs. 6(e)–6(h) gradually become less discernible. In contrast to the AR-PAM images, as shown in Figs. 6(a)–6(d), the enhanced images exhibit significantly improved lateral resolution and clarity. The capillaries indicated by the two white arrows in Figs. 6(a)–6(d) can be well reconstructed by the model. Particularly, in extreme blur scenarios with FWHM values of 75 and 95μm, the blood vessels can also be well reconstructed. Figures 6(a1)–66(d3) and 6(e1)–6(h3) show the two close-up images indicated by the white dashed boxes 1 and 2 in Figs. 6(a)–6(l), respectively. At different levels of FWHM, previously indistinguishable capillaries in the input images due to their proximity are effectively resolved in the output images. Figures 6(m) and 6(n) show the signal distributions of the input images, ground truth, and enhanced images of the white dashed lines in regions 1 and 2 under different FWHM conditions. As the FWHM increases, the blurriness of the input images gradually intensifies, presenting smoother signal curves. However, the signal distribution of the output images exhibits high consistency with the ground truth. These results demonstrate the superior performance of the proposed method in enhancing AR-PAM images under varying degrees of blur.
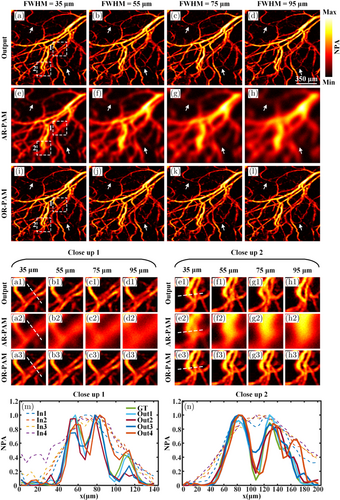
Fig. 6. Reconstruction results under different FWHM. (a)–(d) show the enhanced results of the AR-PAM images with the SNR of 35 dB and the FWHM of 35, 55, 75, and 95μm, respectively. (e)–(h) show the corresponding input images. (i)-(l) show the same ground truth (OR-PAM image). (a1)–(d3) and (e1)–(h3) are the close-up images indicated by the white dashed boxes 1 and 2, respectively. (m) and (n) show the signal distributions indicated by the white dashed lines in the close-up images 1 and 2 under different FWHM. FWHM, full width at half maximum; NPA, normalized photoacoustic amplitude.
Quantitatively, the mean and standard deviation of PSNR and SSIM for 37 test images are computed, as shown in Table 2. At the FWHM of 35μm, the enhanced image exhibits an increase in PSNR of 9.83 dB and an increase in SSIM of 0.29 compared to the input image. As the FWHM increases from 55μm to 95μm with the step size of 20μm, the PSNR of the output image is improved by ∼56%, 63%, and 71% in terms of dB values compared to the input image, respectively. Similarly, the SSIM of the output image is improved by 1.00, 1.48, and 1.70 times, respectively, compared to the input images. These findings suggest that the model exhibits robust applicability and stability across AR-PAM images with different lateral resolutions, and the enhancement of the model is more significant with the deterioration of the lateral resolution.
| Input image | Output image | |||
|---|---|---|---|---|
| FWHM/μm | PSNR/dB | SSIM | PSNR/dB | SSIM |
| 35 | 18.87±1.05 | 0.54±0.078 | 27.81±2.68 | 0.84±0.039 |
| 55 | 16.29±1.13 | 0.37±0.086 | 25.40±2.83 | 0.74±0.069 |
| 75 | 14.44±1.13 | 0.27±0.077 | 23.59±2.84 | 0.67±0.093 |
| 95 | 13.06±1.18 | 0.23±0.074 | 22.38±2.72 | 0.62±0.113 |
3.2.3. Results on different levels of noise
Due to the inevitable presence of noise in real imaging scenarios, Gaussian noise of varying levels is added to AR-PAM images with the FWHM set to 55μm to validate the reconstruction performance of the model under different noise levels. Figures 7(a)–7(d) show the enhanced results of AR-PAM images without noise and with SNR of 35, 25, and 15 dB, respectively. Figures 7(e)–7(h) show the corresponding input images. Figures 7(i)–7(l) show the same ground truth. As the noise level increases, the topological structure of the blood vessels in the AR-PAM images is gradually obscured, and some weak blood vessel signals are submerged by noise (indicated by the white arrows in Figs. 7(e)–7(h)). In contrast, the output images exhibit significantly improved resolution and contrast, with the structural features of the blood vessels being clearly captured and analyzed, even in the indistinct capillaries of the input images (indicated by the white arrows in Figs. 7(a)–7(l)). Figures 7(a1)–7(d3) and 7(e1)–7(h3) present the two close-up images indicated by the white dashed boxes 1 and 2 in Figs. 7(a)–7(l), respectively. Compared to the input images where the vascular structures are indistinguishable, the enhanced results of the model show clearer outlines of the blood vessels and more details, with distinct boundaries between vessels, closely matching the OR-PAM images of the same areas. Figures 7(m) and 7(n) illustrate the signal distributions of the white dashed lines in the close-up images 1 and 2 for input images, ground truth, and enhanced images at different SNR levels. Under varying degrees of noise disturbance, each sharp signal in the output of the model maintains good consistency with the ground truth, demonstrating the superior performance of the proposed method in enhancing the resolution and denoising of AR-PAM images.

Fig. 7. Results of resolution enhancement and denoising under different levels of SNR. (a)–(d) show the enhanced results of the AR-PAM images without noise and with SNR of 35, 25, and 15 dB, respectively, with the FWHM all set to 55μm. (e)–(h) show the corresponding input images. (i)–(l) show the same ground truth (OR-PAM image). (a1)–(d3) and (e1)–(h3) are the close-up images indicated by the white dashed boxes 1 and 2, respectively. (m) and (n) show the signal distributions indicated by the white dashed lines in the close-up images 1 and 2 under different SNR. NPA, normalized photoacoustic amplitude; SNR, signal-to-noise ratio.
Quantitative analysis is conducted based on 37 test images, with the results presented in Table 3. Without noise, the PSNR and the SSIM between the output image and the ground truth are 28.19 dB and 0.84, respectively, whereas the PSNR of the input image is merely 16.35 dB, and the SSIM is only 0.41. The PSNR of the output image is increased by ∼72% in terms of dB value and the SSIM is increased by 2.05 times. For the other noise levels (SNR of 35, 25, and 15 dB), compared with the input images, the PSNR of the output images is improved by ∼56%, 51%, and 66% in terms of dB values, respectively, and the SSIM is improved by 1.00, 1.96, and 4.80 times, respectively. The quantitative data suggest that the proposed method can effectively enhance the resolution of the AR-PAM images across varying degrees of noise disturbance, and the output results exhibit good consistency with the ground truth.
| Input image | Output image | |||
|---|---|---|---|---|
| Noise level | PSNR/dB | SSIM | PSNR/dB | SSIM |
| Without noise | 16.35±1.14 | 0.41±0.100 | 28.19±2.83 | 0.84±0.043 |
| 35 dB | 16.29±1.13 | 0.37±0.086 | 25.40±2.82 | 0.74±0.068 |
| 25 dB | 15.82±1.02 | 0.23±0.048 | 23.94±2.69 | 0.68±0.087 |
| 15 dB | 13.12±0.63 | 0.10±0.011 | 21.79±2.18 | 0.58±0.097 |
3.3. Large-scale mouse brain vasculature data
The experimental results on the sub-images (256×256) of the blood vessels have convincingly demonstrated the feasibility of the model in the lateral resolution enhancement and denoising of the AR-PAM images. Additionally, the complete image of in vivo mouse brain vasculature is used to further verify the enhancement performance of the model on large-scale images. Here, the PAM image of mouse brain vasculature not included in the training is used for evaluation to ensure the effectiveness of the model analysis. The original OR-PAM image has a dimension of 1800×1200 pixels. Initially, the corresponding AR-PAM image is synthesized using Eq. (1), with the FWHM and the SNR set to 55μm and 35 dB, respectively. The image is then cropped into the size of 1456×1056 pixels. To fit the input size of the model, the input image is further cropped into 35 sub-images (256×256), arranged in 5 rows and 7 columns, with 56 pixels assigned as the marginal area. Each sub-image is individually enhanced by the model. Subsequently, all the enhanced sub-images are cropped into the size of 200×200 pixels and then merged into the complete large-scale result with the dimension of 1400×1000 pixels. Afterward, the convertScaleAbs function available in the OpenCV-python library is used for linear brightness adjustment. By employing the ratio of the average brightness of adjacent sub-images and multiplying it by an adjustable factor, brightness inconsistencies in the final merged image are mitigated. The final enhanced result is shown in Fig. 8(a). Figures 8(b) and 8(c) show the AR-PAM image, and the corresponding OR-PAM image, respectively. It can be observed that the topology of the blood vessels in the enhanced result becomes clearer, with superior lateral resolution and enhanced image contrast. Notably, the continuities of the vasculature at the joints of the sub-images are well-maintained, without obvious artifacts. Figures 8(a1)–8(c4) show the close-up images indicated by the white dashed boxes in Figs. 8(a)–8(c), with the signal distribution along the white dashed lines marked in the lower left corner of each image. Compared to the input image, the output image shows richer details of the capillaries, and each sharp signal is more consistent with the ground truth. Vessels in the AR-PAM image that are too close to be distinguished can be clearly recognized in the enhanced image, as shown in Fig. 8(a1). Furthermore, the performance of the resolution enhancement on the large-scale image is quantitatively assessed by calculating the PSNR and SSIM metrics, as shown in the lower right corner of each image. Compared to the ground truth, the PSNR and SSIM of the AR-PAM image are 19.39 dB and 0.53, respectively. In contrast, the PSNR and SSIM of the output image are improved to 24.72 dB and 0.73, respectively, representing increases of ∼27% and 38%. The results indicate that by utilizing the aforementioned cropping and merging strategy, the model can still achieve significant enhancement in the lateral resolution and denoising of large-scale AR-PAM images.

Fig. 8. Result of resolution enhancement for large-scale AR-PAM image. (a) shows the enhancement result of the input image with the SNR of 35 dB and the FWHM of 55μm. (b) shows the corresponding input image. (c) shows the ground truth (OR-PAM image), (a1)–(d3) are the close-up images of the white dashed boxes 1–4 in the corresponding image.
4. Discussion
However, this study has certain limitations. On the one hand, it is challenging to acquire a large dataset of paired OR-AR PAM images with varying noise levels and lateral resolutions using real-world imaging systems. Mainstream PAM systems generally employ point scanning methods, which result in slow imaging speed and make it difficult to obtain large datasets. Even if the same region is imaged, the varying imaging depths of OR-PAM and AR-PAM cause the obtained information to differ. AR-PAM images acquired from deeper tissues typically exhibit greater blurriness, along with reduced SNR and contrast. Therefore, the numerical method was employed to synthesize the simulated AR-PAM images required for network training. Based on the evidence from the point simulation data and the in vivo experimental data under different lateral resolutions and noise levels, the proposed method is reasonably expected to be extendable to enhancing deeper AR-PAM images and applicable to real-world scenarios. While there are limitations to using simulated datasets for training and reconstruction, the powerful generalization capability of the diffusion model32,43,44 ensures that it can still work with in vivo AR-PAM images. Incorporating in vivo experimental data into the dataset will further enhance the performance of the model. On the other hand, the real-time performance of the model is a critical consideration for practical clinical applications. In contrast to the traditional SDE-based diffusion models that require iterations starting from pure noise, the proposed method only starts iterations from the input low-quality image, significantly reducing the reconstruction time and the computational cost, with an average of 6.2 s for 100 iterations on a graphical processing unit (GPU; GeForce RTX 3060Ti). However, how to further reduce the iteration time of the model to achieve the real-time transition from acoustic resolution to optical resolution for AR-PAM images without compromising the reconstruction quality remains a direction for future exploration.
5. Conclusions
In conclusion, a novel mean-reverting diffusion model-aided method was proposed to achieve a balance between the imaging depth and lateral resolution of AR-PAM and OR-PAM. This method significantly transitions the lateral resolution of the AR-PAM images from acoustic resolution toward optical resolution while still preserving its high penetration depth. The proposed method models the degradation process of the OR-PAM image into the noisy version (μ+ϵ) of the low-quality image. Subsequently, the numerical method is employed to iteratively execute reverse-time SDE, aiming to recover the high-quality image from the mean state. Point simulation data and in vivo mouse experimental data were used to evaluate the feasibility of the proposed method regarding the enhancement in lateral resolution and noise elimination of the AR-PAM images under different degradation conditions. The experimental results with the point simulation data quantitatively indicate that the proposed method effectively improves the lateral resolution of the AR-PAM images to better than 15μm under scenarios with varying degrees of noise disturbance. Notably, even in the extreme condition with the FWHM of 55μm and SNR of 15 dB, the proposed method consistently yields high-quality images. The in vivo experimental data, obtained from the real-world system, further demonstrates the superiority of the proposed method. The results indicate that for the AR-PAM image with the FWHM of 35μm and SNR of 35 dB, the PSNR of the enhanced image is improved by 8.94 dB (∼47%), and the SSIM is improved by 0.30 (∼56%). Furthermore, in the extreme condition where the FWHM deteriorates to 95μm, the enhancement of the model becomes even more significant, with the PSNR improved by 9.32 dB (∼71%), and the SSIM improved by 0.39 (∼170%). The enhancement of the lateral resolution on the large-scale AR-PAM image of the in vivo mouse vasculature data further confirms the outstanding performance of the proposed method in volumetric imaging, with the PSNR improved by 5.33 dB (∼0.27) and the SSIM improved by 0.2 (∼0.37). The results of the simulation data and the in vivo data collectively demonstrate the high adaptability and robustness of the model under the conditions of low SNR and lateral resolution, suggesting its potential wide applicability across various physical conditions encountered in AR-PAM imaging scenarios. To enable readers to replicate our results and verify our findings, we have made our code publicly available at https://github.com/yqx7150/PAM-AR2OR.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (62265011 and 62122033), Jiangxi Provincial Natural Science Foundation (20224BAB212006 and 20232BAB 202038), and National Key Research and Development Program of China (2023YFF1204302). The authors thanks Guijun Wang from School of Information Engineering, Nanchang University for helpful discussions. Yiyang Cao, Shunfeng Lu, Cong Wan, and Yiguang Wang are equally contributed to this work.
Conflicts of Interest
The authors declare no conflicts of interest.
ORCID
Yiyang Cao  https://orcid.org/0009-0009-9090-4946
https://orcid.org/0009-0009-9090-4946
Shunfeng Lu  https://orcid.org/0009-0000-0162-645X
https://orcid.org/0009-0000-0162-645X
Cong Wan  https://orcid.org/0009-0008-4943-9459
https://orcid.org/0009-0008-4943-9459
Yiguang Wang  https://orcid.org/0009-0001-7390-6861
https://orcid.org/0009-0001-7390-6861
Xuan Liu  https://orcid.org/0009-0004-7200-5684
https://orcid.org/0009-0004-7200-5684
Kangjun Guo  https://orcid.org/0009-0002-9222-5903
https://orcid.org/0009-0002-9222-5903
Yubin Cao  https://orcid.org/0009-0007-4669-0165
https://orcid.org/0009-0007-4669-0165
Zilong Li  https://orcid.org/0009-0005-5853-5635
https://orcid.org/0009-0005-5853-5635
Qiegen Liu  https://orcid.org/0000-0003-4717-2283
https://orcid.org/0000-0003-4717-2283
Xianlin Song  https://orcid.org/0000-0002-0356-5977
https://orcid.org/0000-0002-0356-5977


