Measuring the Ecological Efficiency of Thermal Power Plants: Evidence from Pakistan
Abstract
This paper assesses the environmental and economic efficiency of thermal plants operating on fossil fuels in Pakistan using methods based on data envelopment analysis. Using the material balance principle, we find that cost- and carbon-efficient points can only be obtained simultaneously by switching to gas. However, under an assumption of variable returns to scale, these points can still be obtained without this conversion through the application of best practices. Furthermore, about 26% of costs and about 34% of carbon emissions can be reduced without a switch to gas, but instead by using technically efficient inputs; this approach can also lead to a significant reduction in electricity prices and considerable environmental benefits. Power plants operating on residual fuel oil are significantly more technically efficient than plants operating on gas. Nonetheless, both types of plants have an equal share in forming the metafrontier as exhibited by the meta-technology ratio. There is a definite need to make plants more efficient by using the best possible combination of inputs and overhauling. Bootstrap results also suggest that further improvement in efficiency is possible.
I. Introduction
Pakistan has faced a severe electricity crisis in recent years. Since 2006, the country has been confronted with power breakages and regular load shedding that lasts for several hours per day. Electricity demand has increased over the years, but power generation has not seen a corresponding increase during the last 2 decades. Many plants are producing electricity below their capacity for the following reasons: (i) a shortage of gas and oil, (ii) circular debt and late payments to electric utilities, and (iii) delayed overhauling.1 As a result, the regular maintenance of power plant machinery, which should take place regularly at intervals of 5 years, generally does not happen. This has led to the deterioration of machinery and a loss of fuel efficiency, resulting in a reduction in plant efficiency and production, and increased fuel costs. Moreover, low efficiency and excessive fuel usage have led to additional carbon dioxide (CO2) emissions and environmental degradation.
In recent years, emphasis has been given to reducing greenhouse gas (GHG) emissions; yet the main obstacle to controlling air pollution is the trade-off between cost and carbon efficiency. Chen, Yeh, and Lee (2013) revealed a significant difference in the efficiency scores obtained by two specifications with and without CO2 emissions under the framework of data envelopment analysis (DEA). Welch and Barnum (2009) explored the wide gap that exists between the cost and carbon efficiency of electric utilities in the United States (US). An increase of 78.9% was found in transitioning from the cost-efficient point to the carbon-efficient point. At the same time, there was an increase of 38% in carbon emissions to transition to the cost-efficient point from the carbon-efficient point. Sarıca and Or (2007) concluded that the empirical relationship between environmental cost and scale efficiency is weak, as indicated by the low R-squared. According to Murty, Kumar, and Dhavala (2007), the technical and environmental inefficiency of thermal power plants in the Indian state of Andhra Pradesh was revealed to be 0.1, which suggested that production could be increased by 10% while reducing the generation of GHGs by 10%.
Electricity generated by thermal plants that use fossil fuels is the main source of global CO2 emissions.2 Furthermore, electricity generation in South Asia mainly depends on fossil fuels. Plants that produce electricity from natural gas are carbon efficient but bear more costs than those plants that are carbon inefficient (Welch and Barnum 2009). However, there may be few firms that are both cost and carbon inefficient; similarly, plants may exist that are both cost and carbon efficient. A key goal of this paper is to explore plants that are simultaneously cost and carbon efficient, as well as plants that are cost and carbon inefficient, under the assumption of variable returns to scale. Furthermore, it is important to find out how much extra cost must be borne to reach the carbon-efficient point. Cost efficiency helps to locate points on the efficient frontier that minimize output while also estimating the potential of cost reduction with current output (Farrell 1957). Färe, Grosskopf, and Lovell (1985) used input prices and the quantity of both inputs and outputs to estimate cost efficiency with linear programming; Camanho and Dyson (2005) introduced a measure of cost efficiency that uses weight-restricted DEA (see Jahanshahloo, Mirdehghan, and Vakili [2011] for an overview of methods and a simplified modeling approach).
Song et al. (2012) highlight three classes of DEA efficiency models that incorporate undesirable outputs. The first class of models treats undesirable outputs as inputs (Berg, Førsund, and Jansen 1992; Hailu and Veeman 2001); however, it does not reveal the true production process at any point (Seiford and Zhu 2002). The second class of models focuses on data transformation into undesirable outputs. Environmental efficiency is then estimated with standard DEA modeling (Seiford and Zhu 2002; Hua, Bian, and Liang 2007). This class of models is solvable only under the variable returns to scale assumption due to convexity constraints (Song et al. 2012). In the third class of models, the disposability of production technology is included in the DEA model (Färe et al. 2005). Given its focus on the output of pollution abatement activities, the directional output distance function is the appropriate DEA model if desirable and undesirable outputs are optimized simultaneously (Chung, Färe, and Grosskopf 1997). The inclusion of the material balance principle (MBP) into the DEA framework relates to the first law of thermodynamics: material inputs are either incorporated into desirable outputs or emitted as undesirable byproducts (Ayres and Kneese 1969). Furthermore, Coelli, Lauwers, and Van Huylenbroeck (2007); Førsund (2009); and Lauwers (2009) introduced the MBP into efficiency analysis for pollution modeling.
The purpose of a DEA efficiency model is to estimate the distance between efficient and actual production points. By doing so, DEA methodology allows the computation of cost efficiency and GHG emissions reduction potential for Pakistan. Moreover, reductions in emissions and cost per unit are not linearly related to the use of fossil fuels but depend on the best market and industry practices that have developed under the assumption of variable returns to scale. The distance of each production unit from the technically efficient point on the production frontier is estimated to determine the degree of technical efficiency. Similarly, the distance of each decision-making unit from the isocost line is estimated to find the cost efficiency, whereas the distance of each production unit from the carbon-efficient point on the isocarbon line is used to identify carbon efficiency. The potential cost and carbon emissions savings are, therefore, determined by the distance to the efficient frontier, which lies at the core of the DEA approach.
Our paper uses the MBP used by Welch and Barnum (2009) for US electric utilities to estimate cost and carbon efficiency. Furthermore, we use the meta-technology ratio previously applied by Seifert, Cullmann, and von Hirschhausen (2016) to German thermal power plants to explore which type of fuel comprises the major share in shaping the technically efficient production frontier. Therefore, our work is the first evaluation study for South Asia (specifically, Pakistan) that comprehensively discusses the ecological efficiency of a power sector that produces electricity from fossil fuels.
Most of the literature has focused on the estimation of technical efficiency or total factor productivity (TFP) change through DEA methods, where undesirable output from these plants was ignored; it was taken either as a negative output or as an additional input, since a cost must be borne to dispose of the undesirable output. In our paper, we provide a method that identifies how both carbon and cost efficiency can be increased simultaneously by changing the combination of carbon inputs, therefore suggesting a novel definition of ecological efficiency.
This paper concentrates on GHG emissions produced by thermal power plants. However, electric utilities operating on fossil fuels emit many other types of gases and substances. While these are not GHGs, they pollute the environment and may pose a significant danger to people's health, including gases such as sulfur dioxide (SO2) and nitrogen oxide (NOx), as well as particulate matter (PM). SO2 may exacerbate heart disease and respiratory illnesses, particularly among children and elderly people. NOx can cause lung diseases, while PM causes hazy conditions and thus asthma, lung cancer, and chronic bronchitis (US EIA 2018). The estimation of CO2 emissions as a result of combustion processes is comparatively simpler as it requires a CO2 emission factor as a function of the fuel property, whereas non-GHG emissions require additional parameters such as the type of technology or boiler, combustion process, fuel properties, operating and maintenance conditions, size of the equipment, and emissions control policy (Amous et al. 2014). Hence, the estimation of non-CO2 emissions requires more data on the production process. Very few studies have been carried out on the estimation of non-CO2 emissions from selected power plants by monitoring engine emissions. Athar, Ali, and Kahn (2010) estimated pollutant emissions by monitoring four thermal power plants for 6 months. They found that emissions were high in the diesel-engine-based power plants, while turbine-based power plants emitted lower levels of pollutants. Sulfur emissions were high under both technologies due to the high sulfur content of the fuel. Ali, Athar, and Ali (2007) estimated non-CO2 emissions by monitoring fossil-fuel-based power plants near Raiwind, Pakistan, with some of the emission parameters being higher than the World Bank standards and National Environment Quality Standards for power plants.
We estimate technical efficiency by assuming variable returns to scale. An estimation of TFP change; technological change; and pure, scale, and technical efficiency changes over time are also considered. This paper has been organized as follows. Section II discusses energy markets and environmental policy in Pakistan. Section III describes data sources and variables. Section IV provides the empirical strategy of the paper. Results are presented in section V. Conclusions and policy recommendations are offered in section VI.
II. Energy Markets and Environmental Policy in Pakistan
In Pakistan, natural gas is less costly and more environmentally friendly than other fossil fuels in terms of power generation (Tables 1 and 2). However, due to shortages and the inaccessibility of natural gas, many plants cannot use it as their fuel input. Thus, the power industry in Pakistan cannot completely switch over to natural gas. Gas prices are not determined by market mechanisms since the Pakistani gas market is fully regulated. The Government of Pakistan is responsible for natural gas pricing as well as for natural gas development, allocation, and distribution. Energy policy determination occurs on the basis of the government's socioeconomic and political agenda rather than profit maximization. Long-term agreements between the government and gas-producing companies constitute the financial basis for the cost of production, which is linked to the international prices of crude oil and high-sulfur fuel oil. Gas companies operating under the gas tariff regime face significant gas losses, which have increased over the last few years.3 This has serious implications for their profits. The Pakistani Oil and Gas Regulatory Authority (OGRA) is the main administrative body for regulating energy markets and activities related to all stages from exploration and development to transmission and distribution. Distribution and transport of natural gas through pipelines is carried out by two public sector companies, the Sui Northern Gas Pipeline Limited and the Sui Southern Gas Company Limited. OGRA sets the price for natural gas upon federal government approval.
| Plant Name | Pollutants and Fuel | SOx | NOx | CO | PM10 |
|---|---|---|---|---|---|
| Attock Gen Limited, Morgah Rawalpindi (165 MW) | RFO | 20 g/s | 67 g/s | 1.7 g/s | |
| Atlas Power, Sheikhupura (225 MW) | RFO | 0.35 t/d MWe (max) | 1,700 ppm | 90 ppm | 70 ppm |
| Nishat Chunian Power (200 MW) | Primary fuel (RFO) | 2,030 mg/Nm3 (max) | 2,000 mg/Nm3 (max) | 100 mg/Nm3 (max) | 110 mg/Nm3 (max) |
| Nishat Power Limited (200 MW) | Primary fuel (RFO) | 2,030 mg/Nm3 (max) | 2,000 mg/Nm3 (max) | 100 mg/Nm3 (max) | 110 mg/Nm3 (max) |
| Engro Energy Limited, Karachi (217 MW) | Natural gas | 54 mg/Nm3 | 79 mg/Nm3 | 103.3 mg/Nm3 | 53.3 mg/Nm3 |
| High-speed diesel | 400 mg/Nm3 | 143 mg/Nm3 | 86.7 mg/Nm3 | 43.3 mg/Nm3 | |
| No. | Fuel | CO2 Emission Factor |
|---|---|---|
| 1 | Bituminous coal and waste coal | 93.3 |
| 2 | Distillate fuel oil | 73.2 |
| 3 | Lignite coal | 97.7 |
| 4 | Natural gas | 53.1 |
| 5 | Residual fuel oil | 78.8 |
Natural gas resources in Pakistan are rapidly depleting. Significant growth in the compressed natural gas (CNG) industry has further widened the gap between demand and supply. Nevertheless, due to the measures taken by the Hydrocarbon Development Institute of Pakistan, the CNG industry has grown significantly. The Government of Pakistan has established various incentives for the growth of this industry in order to provide cost- and environment-efficient fuel for the transportation sector. According to the National Electric Power Regulatory Authority (NEPRA) (2014), the power industry alone requires more than twice the quantity of natural gas than is currently available. The few power plants that can use multiple types of fuel—such as Thermal Power Station Jamshoro (850 megawatts [MW]), Thermal Power Station Muzaffargarh (1350 MW), and Gas Power Station Multan (195 MW)—have to switch to residual fuel oil (RFO) to overcome natural gas shortages. Thermal Power Station Jamshoro has four electricity units, three of which can use either natural gas or oil. However, these three units rely completely on RFO, particularly during winter, due to natural gas shortages.
Due to technological constraints, there are some power plants that cannot easily switch to other fuels. The Government of Pakistan is considering proposals to convert imported oil-fired power plants to liquefied natural gas-fired or coal-fired plants. Specifically, one proposal is the conversion of some power plants from RFO fired to liquefied natural gas fired in order to reduce import dependence, the cost of power generation, and CO2 emissions. A second proposal is to convert some power plants from dual fuel based to coal fired in order to overcome natural gas shortages and reduce the cost of production. The International Monetary Fund, under an agreement with the Government of Pakistan in September 2013, recommended the transition of the power industry from RFO to indigenous natural gas. This measure is necessary to reduce the cost of electricity generation, which stands at 12 rupees (PRs) per unit against the end-user price of PRs9 per unit (Aftab 2014). In this paper, we propose a policy solution that simultaneously reduces both costs and CO2 emissions amid natural gas shortages.
The first ordinance on environmental protection led to the establishment of the Pakistan Environmental Protection Council in 1984. In 1997, Parliament introduced the Pakistan Environmental Protection Act, which created the country's Environmental Protection Agency (EPA). The EPA was granted authority to undertake legal action against environmental polluters. Despite the imposition of national environmental standards in 1999 under the Environmental Protection Act, the World Health Organization, Pakistan Council of Research in Water Resources, and Health Effects Institute have observed that environmental regulations have been ineffective and unable to achieve their goals due to poor implementation (Sohail et al. 2014).
NEPRA has set standards for pollutant emissions by thermal power plants in compliance with national and World Bank environmental quality standards. Table 1 provides NEPRA emissions standards as reported in the licenses of some thermal power plants.
Nevertheless, Ali, Athar, and Ali (2007) and Athar, Ali, and Kahn (2010) argue that most Pakistani thermal plants have failed to comply with the standards of the EPA and NEPRA. The figure indicates seasonal fluctuations in pollutant emissions. Pollutant emissions are high in June and July due to high demand for electricity during these months. Natural gas is more environmentally friendly as it emits lower levels of pollutants than the other fuels. Based on evidence from the licenses of the Jamshoro Company, natural gas has negligible emissions of SO2 and PM. On the other hand, furnace oil produces SO2, NOx, and PM emissions at considerable rates.
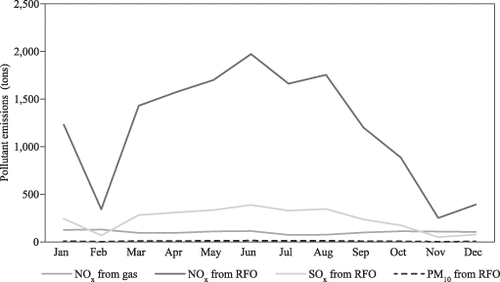
NOx = nitrogen oxide, RFO = residual fuel oil, PM10 = particulate matter (diameter of 10 micrometers), SOx = sulfur oxide.
Evidence from the Global Energy Observatory (2016) shows the territorial distribution of Pakistani thermal power plants, most of which are located in Sindh province and southern Balochistan, as well as in Central and South Punjab. The Northwest Frontier Province of Khyber Pakhtunkhwa as well as the North Punjab and nearby regions are known for their hydropower projects. Emission monitoring stations have been established throughout the country under the government's Clean Air Program. However, plant-level emissions data for Pakistan are not accessible on a full scale (other than what is shown in the figure). Information on the specification of boiler configurations at the unit level and on emission factors for each fuel is not publicly available either. The provision of these datasets would help researchers immensely in estimating pollutant emissions. Policy makers would also be in a position to make more informed decisions toward the achievement of sustainable development goals.
III. Data
Data for Pakistan for 2010–2014 have been collected from the State of Industry reports published by NEPRA. Power System Statistics is an annual publication of the National Transmission and Dispatch Company Limited (2014). The heat content or the calorific value of each fuel—converted from the original units into million British thermal units (MMBTUs)—was gathered from the OGRA and US EIA websites.4 The source of fuel in Pakistan for electricity generation during the review period was domestic natural gas and imported oil from the Gulf countries. Hence, the CO2 emission factor for each fuel has remained stable.
Table 2 shows that natural gas is the most climate-friendly fuel, whereas coal has the highest CO2 emission factor.
The plants covered in this study have more than 13,000 MW of total capacity, or almost two-thirds of the total capacity of all electric utilities in Pakistan, which stood at almost 21,000 MW at the end of 2014. Table 3 indicates that these plants produce almost 59,000 gigawatt hours of electricity. The smallest plant included in this study is Altern Energy Limited in Attock, with only 31 MW capacity, and the largest is Kot Addu Power Company Limited (Privatized) with 1,639 MW capacity. The shares of RFO and natural gas in Pakistan's power generation sector are almost equal. The cost per unit in terms of kilowatt-hour is PRs12.34, but it has a large standard deviation due to differences in fuel prices and technical efficiency. Thermal Power Station Bin Qasim with a capacity of 1,260 MW enjoys the lowest cost per unit at PRs3.29, which makes it the most cost-efficient. The Saba Power Company, Sheikhupura, with a plant capacity of 114 MW, has the highest cost per unit, which results in low cost efficiency.
| Installed Capacity (MW) | Unit Generated (GWh) | Gas Consumed (MMBTU) | RFO Consumed (MMBTU) | Cost per Unit (PRs) | |
|---|---|---|---|---|---|
| Sum | 1.32E+04 | 5.89E+04 | 3.18E+08 | 3.17E+08 | — |
| Average | 3.89E+02 | 1.73E+03 | 9.36E+06 | 9.31E+06 | 1.24E+01 |
| Minimum | 3.10E+01 | 7.60E+01 | 0.00E+00 | 0.00E+00 | 3.69E+00 |
| Maximum | 1.64E+03 | 7.80E+03 | 1.01E+08 | 7.38E+07 | 2.53E+01 |
| SD | 4.33E+02 | 2.00E+03 | 1.94E+07 | 1.70E+07 | 5.53E+00 |
An output-oriented DEA under a variable returns to scale assumption (Banker, Charnes, and Cooper 1984) was applied to the data of 34 plants over a 5-year span. Electricity units generated as the output and fuel consumption (both natural gas and RFO consumption have been added using MMBTU as the unit of analysis), plant capacity, and other costs were kept as the inputs to derive the technical efficiency summary and the Malmquist Index summary.
Table 4 shows that a large majority of thermal plants are working either at increasing returns to scale or decreasing returns to scale. Only five plants are fully efficiently using the scale of the plant. Ten of 13 thermal plants that use RFO as the prime fuel input overutilize the scale of the plant, which in return requires reducing the scale of the plant to be scale efficient. On the other hand, a significant proportion of the plants using gas or both gas and RFO as fuel inputs operate at increasing returns to scale. This may be because in recent years Pakistan faced severe gas shortages, particularly during the winter season. According to NEPRA, the power generation sector is supplied with 133 million cubic feet of gas, while the sector's demand is 372 million cubic feet.
| Increasing Returns to Scale | Constant Returns to Scale | Decreasing Returns to Scale | |
|---|---|---|---|
| Gas | 6 | 3 | 5 |
| Residual fuel oil | 2 | 1 | 10 |
| Gas and residual fuel oil | 5 | 1 | 1 |
| Total | 13 | 5 | 16 |
The scores in Table 5 indicate that the power sector in Pakistan can increase its production by 20.8% according to constant returns to scale technical efficiency and 12.8% according to variable returns to scale technical efficiency without increasing current resources. The scale-efficient point is obtained when a firm or power plant is working at constant returns to scale. Only five plants are fully efficient. Overall, the scale efficiency of the power sector in Pakistan is 0.907. Plants operating on RFO are significantly more efficient than plants operating on natural gas under both the constant returns to scale and variable returns to scale assumptions. The gap between scale-efficient points for constant returns to scale technical efficiency and variable returns to scale technical efficiency for plants using RFO is much smaller than that of plants running on gas. Hence, plants operating on RFO have the highest scale efficiency score.
| Constant RSTE | Variable RSTE | Scale Efficiency | |
|---|---|---|---|
| Gas | 0.760 | 0.836 | 0.904 |
| Residual fuel oil | 0.856 | 0.891 | 0.960 |
| Gas and residual fuel oil | 0.736 | 0.906 | 0.812 |
| Grand mean | 0.792 | 0.872 | 0.907 |
Table 6 indicates that independent power producers are more efficient in Pakistan, according to both the constant returns to scale and variable returns to scale assumptions. The gap between the mean scores of the constant returns to scale technical efficiency and variable returns to scale technical efficiency is trivial for independent power producers because they all operate at either constant returns to scale or close to that level. In contrast, plants working for the Karachi Electric Supply Corporation and the Water and Power Development Authority operate under increasing returns to scale and have a very low scale efficiency score because of a huge gap between their constant returns to scale technical efficiency and variable returns to scale technical efficiency.
| Constant RSTE | Variable RSTE | Scale Efficiency | |
|---|---|---|---|
| Water and Power Development Authority | 0.639 | 0.845 | 0.770 |
| Karachi Electric Supply Corporation | 0.711 | 0.802 | 0.868 |
| Independent power producers | 0.862 | 0.894 | 0.963 |
IV. Methodology
There are various techniques to estimate the ecological efficiency of thermal power plants in Pakistan and these can be both parametric and nonparametric (Berger and Humphrey 1997). DEA and stochastic frontier analysis (SFA) are the two most commonly used approaches to measure the efficiency of decision-making units (DMUs). The former is a nonparametric approach based on linear programming, whereas the latter is a parametric approach requiring a functional form: either a production function or a cost function. DEA is purely deterministic, and the production function is endogenously determined. However, it does not take statistical noise into consideration, thus making it susceptible to noise and measurement error. SFA has the advantage of separating statistical noise from inefficiency. However, it requires assumptions regarding the shape of the production frontier.
The deterministic method has performed relatively better than SFA in panel data analysis, as it is not possible to use SFA in a number of simulations. Moreover, the only advantage of SFA over DEA is that it allows measurement error, which can be overcome in DEA by taking averages with respect to time. This means that SFA has, in fact, no advantage over DEA, whereas DEA holds the advantage of being nonparametric (Ruggiero 2007). Efficiency scores measured by the two approaches have low levels of correlation, whereas technological change scores measured by the two approaches moderately correlate (Odeck 2007). DEA and SFA methods produce conflicting efficiency scores due to measurement issues, the nature of environmental variables, and other random factors (Katharakis, Katharaki, and Katostaras 2014). The bias-corrected DEA estimator proposed by Kneip, Simar, and Wilson (2008) performs best when the efficiency-to-noise variation ratio is large. Furthermore, both DEA and SFA have performed equally well when the efficiency-to-noise variation ratio is equal to 1 (Badunenko, Henderson, and Kumbhakar 2012).
A. Data Envelopment Analysis and Sample Size
According to Boussofiane, Dyson, and Thanassoulis (1991), the minimum number of DMUs required should be equal to the product of the number of outputs and the number of inputs. Dyson et al. (2001), however, stated that sample size should be at least greater than or equal to twice the product of inputs and outputs. Golany and Roll (1989) recommended that the number of DMUs must be at least twice the sum of inputs and outputs, while Bowlin (1998) argued that the sample size should be at least three times the sum of inputs and outputs. On the one hand, a large sample size increases the probability of capturing high-performance production units that determine the efficient frontier; on the other hand, it may reduce the homogeneity of the dataset (Golany and Roll 1989). Our study uses a sample size based on all the criteria mentioned above in order to achieve sufficient discriminatory power. Furthermore, we implement bootstrap DEA as per Simar and Wilson (2000) that corrects bias as a result of a small sample size (for an overview of methods, see Sarkis [2007]).
B. Malmquist Productivity Index
The TFP change over time can be estimated using the Malmquist Productivity Index, which is based on linear programming within the DEA framework. This method has the capability of dealing with multiple inputs and outputs; it associates productivity change with the effects of economies of scale (Hollas, Macleod, and Stansell 2002). The Malmquist Productivity Index was presented by Färe, Grosskopf, and Tyteca (1996) as
The above equation shows the productivity of production point (Yt+1,Xt+1) relative to production point (Xt,Yt). If its value is greater than 1, it shows a positive TFP change from the current period (t) to the next period (t+1). The TFP change can be less than, greater than, or equal to 1. If it takes a value equal to 1, then it shows no change in TFP. If it is larger than 1, then it suggests an increase; if less than 1, it postulates a drop in TFP. Per Färe et al. (1992, p. 90–96), “the total factor productivity is the product of technical efficiency change and technological change, whereas technical efficiency change can be further divided into pure efficiency change and scale efficiency change.” Scale efficiency shows whether a firm operates at the peak productive scale size (Bruno and Erbetta 2014). A scale efficiency score of less than unity indicates that a firm is underutilizing or overutilizing the scale of the plant. Efficiency that compares DMUs of the same scale is called pure technical efficiency (Farrell 1957). Technical efficiency refers to the production point that gives maximum output with minimum possible inputs. It is located on the isoquant, or the production frontier. The degree by which the level of production of a DMU or a production unit approaches its maximum level of production is termed technical efficiency (Färe and Lovell 1978).
C. Environmental Efficiency and Data Envelopment Analysis
Since environmental degradation has become one of the most pressing issues in human development, the incorporation of environmental factors into efficiency analysis has become a key element of research. In this paper, we include environmental factors into the DEA, as the latter can deal with multiple outputs and does not require a specific function form (Berger and Humphrey 1997). Färe, Grosskopf, and Tyteca (1996) introduced an activity analysis model and applied it to US electric utilities. Furthermore, they compared that model with the more conventional pollution index of Jaggi and Freedman (1992). The TFP is decomposed into input efficiency, output efficiency, and a pollution index to compute an environmental performance indicator. Korhonen and Luptácik (2004) introduced the concept of eco-efficiency into DEA. Metafrontier DEA was used by Seifert, Cullmann, and von Hirschhausen (2016) to estimate the reduction of CO2 emissions and energy-saving potential. The material balance condition was introduced by Coelli, Lauwers, and Van Huylenbroeck (2007) and later used by Welch and Barnum (2009) to explore the costs and carbon efficiency of US electric utilities.
The introduction of the MBP is relevant, as this approach not only explores the ecological efficiency of thermal plants, but also helps the DMUs to locate the production point that could simultaneously reduce cost and carbon emissions. Furthermore, this method identifies the best combination of fossil fuel inputs where the gap between cost and carbon efficiency is minimized. In this method, carbon efficiency is estimated by treating the CO2 emission factor for each fuel like a price (Coelli, Lauwers, and Van Huylenbroeck 2007). It is important to point out that the MBP has not been included in many production and environmental models (Lauwers 2009). According to Pethig (2003), the absence of MBP methodology from production and environmental policy analysis may lead to incorrect policy advice. An improvement in technical efficiency can simultaneously reduce both cost and emissions. This simultaneous reduction rejects the notion of early environmentally adjusted productivity analysis that emissions reduction is costly (Lauwers 2009).
According to Coelli, Lauwers, and Van Huylenbroeck (2007), a DMU produces a vector of m = 1, 2,…, M outputs, y∈RM+, using a vector of k = 1, 2,… , K inputs, x∈RM+. The achievable production set, T, is defined as
and
D. Meta-Technology Ratio
Battese, Rao, and O'Donnell (2004) introduced the concept of the meta-technology ratio as the technology gap ratio. It is the ratio of the group frontier technical efficiency score to the metafrontier efficiency score. According to this method, technical efficiency scores are first obtained by applying DEA to the group of DMUs or the firms having the same technology (Zhu and Cook 2007). In our paper, three plant types are defined: (i) plants that use RFO as the only fuel, (ii) plants that use gas as the only fuel, and (iii) plants that use both gas and RFO as their fuel inputs. In the second stage, DEA is applied to the combined data of thermal plants from all the technologies. Since this ratio lies between 0 and 1, the higher the value of the technology gap ratio, the lower the gap with the most efficient technology. To avoid any ambiguity, the concept of the technology gap ratio was renamed as the meta-technology ratio by O'Donnell, Rao, and Battese (2008).
E. Bootstrapping Data Envelopment Analysis
Bootstrapping in DEA was introduced by Simar and Wilson (1998, 2000). The properties of DEA bootstrapping are defined by Kneip, Simar, and Wilson (2008). DEA bootstrapping is performed in three steps. First, a random subsample is drawn from the original sample with replacement, uniformly and independently. In the second step, DEA estimation is performed on the subsample. Finally, a large number of repetitions is required to obtain bias-corrected efficiency scores (Kneip, Simar, and Wilson 2008).
With the help of DEA bootstrapping, it is possible to draw an inference and calculate the confidence interval. Moreover, the bias in efficiency scores may also be corrected by the DEA bootstrapping approach. The true data-generating process for bootstrapping is defined as
The above-mentioned sample can be drawn from the data-generating process ˆP=P(ˆT,ˆf(x,y)). The true world ˆθDEA is an estimate of the unknown θ based on Xn, whereas in the bootstrap world ˆθ*DEA is an estimator for ˆθ*DEA based on X*n:
V. Results
A. Malmquist Data Envelopment Analysis
As the results in Table 6 indicate, TFP increased by almost 64% in 2011, mainly because of a sharp improvement in technology of about 87% and despite a fall of about 13% in technical efficiency. Technical efficiency improved by about 21% in the next year, predominantly because of an improvement in scale efficiency and marginally because of an improvement in pure efficiency. TFP and efficiency remained unchanged in 2013. On average, an increase of 3.9% in technical efficiency was recorded every year in the given period. TFP increased by almost 12% on average each year, largely because of an annual improvement in technology of 7.9%.
As Table 7 suggests, plants operating on RFO enhanced their TFP by more than 9%, mainly attributable to a more than 7% improvement in technology. The efficiency change in plants running on RFO is negligible on average. Plants operating on gas showed an increase of more than 13% in their TFP because of improvements of more than 5% and 7% in efficiency and technology, respectively. Plant-level results are given in Appendix Table A1.
| Year | Efficiency Change | Technological Change | Pure Efficiency Change | Scale Efficiency Change | TFP Change |
|---|---|---|---|---|---|
| 2011 | 0.877 | 1.874 | 1.003 | 0.874 | 1.643 |
| 2012 | 1.213 | 0.817 | 1.06 | 1.145 | 0.991 |
| 2013 | 1.006 | 0.971 | 0.995 | 1.011 | 0.977 |
| 2014 | 1.088 | 0.911 | 1.004 | 1.084 | 0.992 |
| Mean gas | 1.055 | 1.074 | 1.031 | 1.023 | 1.136 |
| Mean RFO | 1.018 | 1.076 | 1.011 | 1.008 | 1.096 |
| Mean gas and RFO | 1.055 | 1.105 | 0.998 | 1.057 | 1.170 |
| Mean | 1.039 | 1.079 | 1.015 | 1.023 | 1.121 |
B. Material Balance Condition
A cost data envelopment analysis was implemented on a dataset of 5-year averages, keeping electricity units generated in gigawatt hours as the output and gas and RFO consumption in MMBTU as the two inputs. Annual averages of the variables were taken, thus helping to minimize the measurement error (Ruggiero 2007). The cost DEA was run in two different ways: first, with the isocost line and by using average prices of gas and RFO; second, with the isocarbon line and by using the CO2 emission factor for the fuels. The material balance approach was implemented in four steps. First, technically efficient inputs were estimated by multiplying actual quantity of inputs by the value of technical efficiency. Second, the cost DEA was run using the prices of each fuel. Third, carbon efficiency was estimated using the CO2 emission factor of each fuel. Finally, the technically efficient inputs were multiplied by the prices and CO2 emission factors to estimate how much the respective costs and carbon emissions could be reduced by transitioning toward the technically efficient point.
As Table 8 shows, the power sector in Pakistan, which relies on fossil fuels, is highly cost and carbon inefficient. The cost-efficient point can be reached by using almost 60% fewer fuel inputs, whereas the carbon-efficient point could be obtained by consuming almost 48% fewer fuel inputs. In Pakistan, gas is also cheaper than RFO because it is extracted from within the country, whereas RFO is by and large imported from Gulf countries. At the same time, gas also has a lower CO2 factor than RFO, thus there is no trade-off between cost and carbon efficiency. The carbon-efficient point can be reached by using cost-minimizing inputs as revealed by the results of DEA. There is a certain necessity to switch to the technology that uses gas as the prime input. In any case, the cost- and carbon-efficient points can even be reached by plants using RFO as the only input, as demonstrated by Plant 13 in Appendix Table A2.1. Plants 8, 12, and 13 are the only super-efficient plants that are simultaneously cost and carbon efficient as indicated in Table A1.2.
| Cost DEA with Price Specification | Efficiency Scores with Isocarbon Line | |||||
|---|---|---|---|---|---|---|
| Plant | Technical Efficiency | Allocative Efficiency | Cost Efficiency | Technical Efficiency | Allocative Efficiency | Carbon Efficiency |
| Mean | 0.728 | 0.591 | 0.393 | 0.728 | 0.748 | 0.520 |
Plants using gas as the only input have low cost and carbon efficiency, owing to low technical efficiency despite being allocatively efficient, whereas plants using RFO as their prime input have low cost and carbon efficiency because of their low allocative efficiency. In Table A2, Plant 13 is the only plant using RFO as the only fuel input, but it is completely allocatively efficient and shows that a thermal plant operating on RFO can be cost and carbon efficient at the same time.
Technically efficient inputs and output were obtained by implementing a single-stage DEA on the data with electricity production as the output and natural gas and RFO consumption as inputs. The target output is almost the same as the actual output due to using an input-oriented DEA, which minimizes the cost (or level) of inputs at given outputs. Achieving cost- and carbon-efficient points in Pakistan is highly difficult because it requires an almost complete switch to power production entailing the use of gas as the only fuel. Since Pakistan faced a severe gas shortage in recent years that almost shut down the CNG industry and severely affected the industrial, household, and commercial sectors, switching production technology to gas will be a challenging task in the short run. Moreover, switching to gas may also require modifications in plant design. Nevertheless, even without changing the production technology, plants can still reduce a significant amount of their costs and carbon emissions, and increase their cost and carbon efficiency, as shown in Table 9.
| Fuel Type | Technical Efficiency | Allocative Efficiency | Cost Efficiency | Technical Efficiency | Allocative Efficiency | Carbon Efficiency |
|---|---|---|---|---|---|---|
| Gas | 0.621 | 1.000 | 0.621 | 0.621 | 1.000 | 0.621 |
| RFO | 0.885 | 0.280 | 0.256 | 0.885 | 0.552 | 0.496 |
| Gas and RFO | 0.650 | 0.349 | 0.191 | 0.650 | 0.607 | 0.366 |
As the results in Table 10 show, natural gas use can be reduced by about 61% by achieving a technically efficient point. Furthermore, about 16% of RFO consumption can be reduced. Almost 39% of fuel consumption can be cut and approximately 36% of the heat rate can be reduced. Fuel costs can be cut by about 26%, which would ultimately lead to a significant fall in electricity prices. Most interestingly, carbon emissions can be reduced by about 33%, which would be a boon to the environment. Table 10 also shows that cost and carbon efficiency can be boosted by significant proportions as well. Plant-level results are reported in Appendix Table A2.2.
| Original | Technically Efficient | Percentage Change (%) | |
|---|---|---|---|
| Gas consumption | 3.18E+08 | 1.24E+08 | −61.2 |
| RFO consumption | 3.17E+08 | 2.66E+08 | −16.1 |
| Fuel consumption | 6.35E+08 | 3.89E+08 | −38.7 |
| Average heat rate | 1.16E+04 | 7.45E+03 | −36.0 |
| Fuel cost | 6.15E+11 | 4.54E+11 | −26.2 |
| CO2 emissions | 2.59E+07 | 1.74E+07 | −32.8 |
| Cost efficiency | 3.90E–01 | 5.90E–01 | 50.4 |
| Carbon efficiency | 5.20E–01 | 7.50E–01 | 43.9 |
C. Group and Metafrontier Data Envelopment Analysis
In this section, overall eco-efficiency is explored by keeping electricity produced and CO2 emissions as the outputs, while fuel consumption, plant capacity, and other costs are the inputs. Efficiency scores were obtained in two different ways: first, by applying an input-oriented data envelopment analysis, known as the metafrontier DEA, to all 34 plants; second, by applying a group frontier DEA, which is also an input-oriented DEA, to three different types of plants (gas, RFO, and gas and RFO) separately. Meta-technology ratios were obtained by dividing the metafrontier efficiency scores by the group frontier efficiency scores.
By and large, Table 11 shows a similar pattern of the returns to scale as discussed in section I.
| Increasing Returns to Scale | Constant Returns to Scale | Decreasing Returns to Scale | |
|---|---|---|---|
| Gas | 6 | 3 | 5 |
| Residual fuel oil | 2 | 2 | 9 |
| Gas and residual fuel oil | 6 | 1 | 0 |
| Total | 14 | 6 | 14 |
Similar to the results of output-oriented DEA, the metafrontier results shown in Table 12 reveal that plants operating on RFO are more efficient, with an efficiency score of 0.85. However, the gap between the mean efficiency of plants operating on RFO and gas is narrowed due to the higher CO2 factor of RFO. The group frontier DEA of the RFO plants also provides interesting results because the efficiency of RFO again appears to be the highest.
| Metafrontier DEA | Group Frontier DEA | |||||
|---|---|---|---|---|---|---|
| Fuel Type | Constant RSTE | Variable RSTE | Scale Efficiency | Constant RSTE | Variable RSTE | Scale Efficiency |
| Gas | 0.807 | 0.862 | 0.930 | 0.929 | 0.965 | 0.961 |
| RFO | 0.857 | 0.894 | 0.957 | 0.990 | 0.997 | 0.993 |
| Gas and RFO | 0.753 | 0.949 | 0.798 | 0.898 | 0.949 | 0.945 |
| Grand Mean | 0.815 | 0.892 | 0.913 | |||
Although plants operating on RFO tend to be more efficient, Table 13 shows that the metafrontier technology ratio for both plant types is similar, which implies that they both have a significant share in the metafrontier.
| Constant RSTE | Variable RSTE | Scale Efficiency | |
|---|---|---|---|
| Gas | 0.869 | 0.893 | 0.967 |
| Residual fuel oil | 0.866 | 0.896 | 0.964 |
| Gas and residual fuel oil | 0.839 | 1.000 | 0.845 |
Table 14 reports the results of bootstrapping. A total of 2,000 bootstrap replications were performed in each case. In the case of 1 output (electricity generation) and 3 inputs (fuel consumption, plant capacity, and miscellaneous cost), where the replications are performed on panel data containing 170 observations, the bias is slightly above 2%, which suggests that bias-corrected technical efficiency scores are about 2% less than the scores calculated without bootstrapping. However, for 1 output (electricity generation) and 2 inputs (gas and RFO consumption), where the replications are performed on annual averages containing 34 observations, the bias is 4.4% and 7.4% for without replacement and with replacement sampling, respectively.
| Type of Sampling | Scale Assumption | N | B | Mean TE | CIL | CIU | TEBC | Bias | Specification |
|---|---|---|---|---|---|---|---|---|---|
| With replacement | CRS | 170 | 2000 | 0.6547 | 0.5958 | 0.6547 | 0.6341 | 0.0206 | 1 output 3 inputs |
| Without replacement | CRS | 100 | 2000 | 0.6547 | 0.5743 | 0.6547 | 0.6362 | 0.0202 | 1 output 3 inputs |
| With replacement | VRS | 170 | 2000 | 0.7788 | 0.6967 | 0.7788 | 0.7582 | 0.0206 | 1 output 3 inputs |
| Without replacement | VRS | 100 | 2000 | 0.7788 | 0.6708 | 0.7788 | 0.7577 | 0.0211 | 1 output 3 inputs |
| With replacement | CRS | 34 | 2000 | 0.5612 | 0.4521 | 0.5612 | 0.4870 | 0.0742 | 1 output 2 inputs |
| Without replacement | CRS | 25 | 2000 | 0.5612 | 0.4454 | 0.5612 | 0.5169 | 0.0443 | 1 output 2 inputs |
V. Conclusions and Policy Implications
In this paper, we apply various methods of DEA. In Pakistan, natural gas is an ideal fuel to achieve the goal of cost and carbon minimization simultaneously. However, both carbon and cost efficiency can also be achieved by using RFO as the only input combined with best practices and optimal plant use under the assumption of variable returns to scale. Plants running on RFO are technically more efficient than plants operating on gas. Hence, there is a need to reduce the price of RFO to make RFO plants more cost-efficient. Second, it is imperative to import gas either through a pipeline or in the form of liquid petroleum gas so that the plants can obtain an uninterrupted supply of gas and make better and more efficient use of scale. Since plants in Pakistan are highly technically inefficient, there is a need to overhaul these plants to improve their technical efficiency so that they can reduce both costs and CO2 emissions. According to NEPRA (2014), overhauls must be carried out every 5 years, whereas in Pakistan, the overhauling of most plants has been delayed by more than a decade.
Pollutant emissions can be reduced significantly by burning low-sulfur coal, using PM emission control devices and fluidized-bed combustion technology to control SO2 emissions, and introducing low-NOx burners during the combustion phase (US EIA 2018). More research can be done toward identifying pollutant efficiency as well as the effectiveness of pollution control policies and technologies. Since thermal power plants in Pakistan are highly technically inefficient, producing at technically efficient points on the isoquant can simultaneously reduce both costs and carbon emissions significantly. A reduction in carbon emissions can generate positive externalities in relation to a cleaner environment and a better climate, while significant cost reductions will result in lower electricity tariffs and less import dependence for Pakistan's economy. Reducing electricity tariffs can have further positive effects on consumer welfare and industrial growth by lowering the cost of doing business.
Notes
1 The State of Industry is an annual report compiled by the National Electric Power Regulatory Authority. The report analyzes the status of power generation, distribution, and demand in Pakistan each year, and it elaborates on the various challenges facing the energy sector.
2 Center for Climate and Energy Solutions. Global Emissions. https://www.c2es.org/content/international-emissions/.
3 Under the gas tariff regime, OGRA determines the tariffs of all regulated activities under the OGRA ordinance issued in 2002 (OGRA 2017). The difference between the total volume of the gas supplied and the gas volume sold or billed is defined as “unaccounted for gas” (Sui Northern Gas Training Institute 2016).
4 The data on the heat rate of each plant is computed using the following US EIA formula: Heatrate=totalfuelinputsinMMBTUtotaloutputinkWh. Heat rate is the amount of energy that a plant requires to produce 1 kilowatt-hour of electricity (US EIA 2016). Total CO2 emissions per 1 kilowatt-hour of electricity are calculated by dividing the product of the CO2 emission factor for each fuel per MMBTU and the heat rate by 1 million.
Appendix 1
| Fuel Type | Firm | Efficiency Change | Techno-logical Change | Pure Efficiency Change | Scale Efficiency Change | TFP Change |
|---|---|---|---|---|---|---|
| Gas | 5 | 1.109 | 1.023 | 1.000 | 1.109 | 1.135 |
| Gas | 6 | 1.096 | 1.195 | 1.106 | 0.991 | 1.311 |
| Gas | 8 | 1.126 | 1.144 | 1.066 | 1.056 | 1.288 |
| Gas | 9 | 1.145 | 1.103 | 1.090 | 1.050 | 1.263 |
| Gas | 10 | 1.180 | 1.129 | 1.102 | 1.071 | 1.331 |
| Gas | 11 | 1.001 | 1.024 | 1.000 | 1.001 | 1.025 |
| Gas | 12 | 1.053 | 1.074 | 1.041 | 1.012 | 1.131 |
| Gas | 16 | 1.028 | 1.079 | 1.036 | 0.992 | 1.110 |
| Gas | 17 | 1.082 | 1.137 | 1.080 | 1.002 | 1.230 |
| Gas | 19 | 1.081 | 1.081 | 1.070 | 1.010 | 1.169 |
| Gas | 23 | 0.860 | 1.067 | 0.861 | 0.999 | 0.918 |
| Gas | 27 | 0.995 | 1.091 | 0.996 | 1.000 | 1.086 |
| Gas | 30 | 1.014 | 0.952 | 1.000 | 1.014 | 0.965 |
| Gas | 32 | 1.002 | 0.941 | 0.992 | 1.011 | 0.943 |
| Mean | 1.055 | 1.074 | 1.031 | 1.023 | 1.136 | |
| RFO | 13 | 1.029 | 1.102 | 1.018 | 1.011 | 1.134 |
| RFO | 14 | 1.001 | 1.102 | 0.990 | 1.012 | 1.103 |
| RFO | 15 | 1.020 | 1.086 | 1.020 | 1.000 | 1.108 |
| RFO | 18 | 1.092 | 1.086 | 1.074 | 1.017 | 1.186 |
| RFO | 20 | 0.976 | 1.103 | 0.971 | 1.005 | 1.076 |
| RFO | 21 | 0.992 | 1.030 | 0.971 | 1.022 | 1.022 |
| RFO | 24 | 0.941 | 1.009 | 0.934 | 1.008 | 0.949 |
| RFO | 25 | 1.051 | 1.104 | 1.038 | 1.013 | 1.160 |
| RFO | 26 | 1.000 | 1.074 | 1.000 | 1.000 | 1.074 |
| RFO | 28 | 0.969 | 0.965 | 0.969 | 1.000 | 0.935 |
| RFO | 29 | 1.105 | 0.960 | 1.095 | 1.009 | 1.060 |
| RFO | 33 | 1.033 | 1.195 | 1.027 | 1.006 | 1.235 |
| RFO | 34 | 1.030 | 1.170 | 1.033 | 0.998 | 1.205 |
| Mean | 1.018 | 1.076 | 1.011 | 1.008 | 1.096 | |
| Gas and RFO | 1 | 1.171 | 1.104 | 1.000 | 1.171 | 1.293 |
| Gas and RFO | 2 | 1.035 | 1.173 | 1.000 | 1.035 | 1.215 |
| Gas and RFO | 3 | 1.094 | 1.208 | 1.039 | 1.053 | 1.321 |
| Gas and RFO | 4 | 1.096 | 1.128 | 1.030 | 1.064 | 1.236 |
| Gas and RFO | 7 | 1.070 | 1.157 | 1.006 | 1.064 | 1.239 |
| Gas and RFO | 22 | 0.921 | 1.067 | 0.911 | 1.011 | 0.983 |
| Gas and RFO | 31 | 1.000 | 0.901 | 1.000 | 1.000 | 0.901 |
| Mean | 1.055 | 1.105 | 0.998 | 1.057 | 1.170 | |
| Grand mean | 1.039 | 1.079 | 1.015 | 1.023 | 1.121 |
Appendix 2
| Cost DEA with Price Specification | Efficiency Scores with Isocarbon Line | ||||||
|---|---|---|---|---|---|---|---|
| Plant | Technical Efficiency | Allocative Efficiency | Cost Efficiency | Technical Efficiency | Allocative Efficiency | Carbon Efficiency | Fuel Type |
| 1 | 0.652 | 0.314 | 0.205 | 0.652 | 0.705 | 0.460 | Gas and RFO |
| 2 | 1.000 | 0.312 | 0.312 | 1.000 | 0.726 | 0.726 | Gas and RFO |
| 3 | 0.771 | 0.132 | 0.102 | 0.771 | 0.307 | 0.237 | Gas and RFO |
| 4 | 0.321 | 0.902 | 0.290 | 0.321 | 0.980 | 0.315 | Gas and RFO |
| 5 | 0.179 | 1.000 | 0.179 | 0.179 | 1.000 | 0.179 | Gas |
| 6 | 0.555 | 1.000 | 0.555 | 0.555 | 1.000 | 0.555 | Gas |
| 7 | 0.558 | 0.212 | 0.119 | 0.558 | 0.457 | 0.255 | Gas and RFO |
| 8 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | Gas |
| 9 | 0.838 | 1.000 | 0.838 | 0.838 | 1.000 | 0.838 | Gas |
| 10 | 0.654 | 1.000 | 0.654 | 0.654 | 1.000 | 0.654 | Gas |
| 11 | 0.767 | 1.000 | 0.767 | 0.767 | 1.000 | 0.767 | Gas |
| 12 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | Gas |
| 13 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | RFO |
| 14 | 0.811 | 0.163 | 0.132 | 0.811 | 0.381 | 0.309 | RFO |
| 15 | 0.811 | 0.162 | 0.131 | 0.811 | 0.378 | 0.306 | RFO |
| 16 | 0.998 | 1.000 | 0.998 | 0.998 | 1.000 | 0.998 | Gas |
| 17 | 0.598 | 1.000 | 0.598 | 0.598 | 1.000 | 0.598 | Gas |
| 18 | 0.813 | 0.232 | 0.189 | 0.813 | 0.542 | 0.440 | RFO |
| 19 | 0.634 | 1.000 | 0.634 | 0.634 | 1.000 | 0.634 | Gas |
| 20 | 1.000 | 0.294 | 0.294 | 1.000 | 0.687 | 0.687 | RFO |
| 21 | 0.879 | 0.217 | 0.191 | 0.879 | 0.507 | 0.445 | RFO |
| 22 | 0.251 | 0.352 | 0.088 | 0.251 | 0.677 | 0.170 | Gas and RFO |
| 23 | 0.543 | 1.000 | 0.543 | 0.543 | 1.000 | 0.543 | Gas |
| 24 | 0.869 | 0.280 | 0.244 | 0.869 | 0.654 | 0.569 | RFO |
| 25 | 0.922 | 0.278 | 0.256 | 0.922 | 0.649 | 0.598 | RFO |
| 26 | 0.790 | 0.224 | 0.177 | 0.790 | 0.523 | 0.414 | RFO |
| 27 | 0.548 | 1.000 | 0.548 | 0.548 | 1.000 | 0.548 | Gas |
| 28 | 0.977 | 0.194 | 0.19 | 0.977 | 0.453 | 0.442 | RFO |
| 29 | 0.751 | 0.185 | 0.139 | 0.751 | 0.431 | 0.324 | RFO |
| 30 | 0.157 | 1.000 | 0.157 | 0.157 | 1.000 | 0.157 | Gas |
| 31 | 1.000 | 0.220 | 0.220 | 1.000 | 0.396 | 0.396 | Gas and RFO |
| 32 | 0.216 | 1.000 | 0.216 | 0.216 | 1.000 | 0.216 | Gas |
| 33 | 1.000 | 0.209 | 0.209 | 1.000 | 0.487 | 0.487 | RFO |
| 34 | 0.883 | 0.205 | 0.181 | 0.883 | 0.477 | 0.421 | RFO |
| Mean | 0.728 | 0.591 | 0.393 | 0.728 | 0.748 | 0.520 | |
| Plant | Target Electricity Production (GWh) | Target Gas Consumption (MMBTU) | Target RFO Consumption (MMBTU) | Fuel Cost Reduction | CO2 Reduction | Cost Efficiency | Carbon Efficiency |
|---|---|---|---|---|---|---|---|
| 1 | 160 | 155,034 | 1,527,600 | 34.762 | 34.803 | 0.314 | 0.705 |
| 2 | 76 | 6,763 | 1,364,908 | 0 | 0 | 0.312 | 0.726 |
| 3 | 4,515 | 236,187 | 40,571,308 | 22.871 | 22.878 | 0.132 | 0.307 |
| 4 | 1,832 | 7,818,473 | 362,475 | 67.863 | 67.863 | 0.902 | 0.980 |
| 5 | 4,386 | 18,085,622 | 0 | 82.113 | 82.113 | 1.000 | 1.000 |
| 6 | 353 | 2,456,765 | 0 | 44.539 | 44.539 | 1.000 | 1.000 |
| 7 | 2,577 | 3,244,823 | 14,121,228 | 44.175 | 44.171 | 0.212 | 0.457 |
| 8 | 100 | 1,476,328 | 0 | 0 | 0 | 1.000 | 1.000 |
| 9 | 196 | 1,848,351 | 0 | 16.193 | 16.022 | 1.000 | 1.000 |
| 10 | 504 | 3,041,926 | 0 | 34.556 | 34.504 | 1.000 | 1.000 |
| 11 | 356 | 2,468,390 | 0 | 23.264 | 23.307 | 1.000 | 1.000 |
| 12 | 6,222 | 25,200,569 | 0 | 0 | 0 | 1.000 | 1.000 |
| 13 | 7,796 | 0 | 73,767,491 | 0 | 0.003 | 1.000 | 1.000 |
| 14 | 1,754 | 0 | 13,934,887 | 18.890 | 18.899 | 0.163 | 0.381 |
| 15 | 1,797 | 0 | 14,360,707 | 18.919 | 18.910 | 0.162 | 0.378 |
| 16 | 182 | 1,794,098 | 0 | 0.184 | 0.404 | 1.000 | 1.000 |
| 17 | 1,149 | 5,541,458 | 0 | 40.157 | 40.147 | 1.000 | 1.000 |
| 18 | 564 | 0 | 4,070,854 | 18.747 | 18.776 | 0.232 | 0.542 |
| 19 | 755 | 4,014,613 | 0 | 36.608 | 36.624 | 1.000 | 1.000 |
| 20 | 210 | 0 | 1,865,036 | 0 | 0 | 0.294 | 0.687 |
| 21 | 826 | 0 | 5,703,409 | 12.072 | 12.072 | 0.217 | 0.507 |
| 22 | 1,160 | 2,516,996 | 3,856,725 | 74.851 | 74.856 | 0.352 | 0.677 |
| 23 | 2,865 | 12,191,376 | 0 | 45.717 | 45.720 | 1.000 | 1.000 |
| 24 | 252 | 0 | 2,126,743 | 13.073 | 13.004 | 0.280 | 0.654 |
| 25 | 260 | 0 | 2,176,592 | 7.811 | 7.953 | 0.278 | 0.649 |
| 26 | 679 | 0 | 4,787,433 | 20.951 | 20.974 | 0.224 | 0.523 |
| 27 | 4,146 | 17,155,563 | 0 | 45.208 | 45.213 | 1.000 | 1.000 |
| 28 | 1,221 | 0 | 8,656,705 | 2.306 | 2.338 | 0.194 | 0.453 |
| 29 | 1,333 | 0 | 9,765,816 | 24.873 | 24.873 | 0.185 | 0.431 |
| 30 | 1,390 | 6,475,392 | 0 | 84.330 | 84.332 | 1.000 | 1.000 |
| 31 | 6,304 | 3,749,075 | 47,799,321 | 0 | 0 | 0.220 | 0.396 |
| 32 | 773 | 4,084,367 | 0 | 78.429 | 78.424 | 1.000 | 1.000 |
| 33 | 1,087 | 0 | 7,329,732 | 0 | 0 | 0.209 | 0.487 |
| 34 | 1,121 | 0 | 7,666,427 | 11.745 | 11.761 | 0.205 | 0.477 |


