Entropy analysis of Casson nanofluid flow across a rotating porous disc with nonlinear thermal radiation and magnetic dipole
Abstract
The theme of the current effort is to theoretically analyze the entropy generation and heat transfer aspects of Casson nanofluid flow triggered by rotating porous disc with the presence of magnetic dipole, nonlinear thermal radiation, viscous dissipation and Joule heating. The modeling of the nanofluid can be described with the combination of Brownian motion and thermophoresis by incorporating the passive control boundaries, and the governing PDEs are transformed into a set of highly nonlinear ODEs. The resulting equations are then solved analytically using HAM technique. The present results are compared with previously published results, which are in excellent agreement. The effect of pertinent nondimensional parameters on the entropy generation, hydrodynamic, heat and mass transport aspects is discussed via graphical illustrations. Both radial and tangential velocities are affected by accelerating the values of Hartmann number and porosity parameter. The temperature profile is upsurged by improving the radiation and thermal ratio parameter. Increasing the Casson parameter and Brinkman number leads to improved entropy generation rate. Moreover, skin friction, heat and mass transfer rates are examined with the help of the tables. It is believed that this study can be utilized as coolants by numerous automotive and engineering industries, namely the electronic devices, electrical motor, spin coating, fabrication of spacecraft, thermal insulation, nuclear reactors, etc.
Nomenclature
| : | Cylindrical coordinates | |
| m | : | Thickness of index |
| : | Ferro magnetic interaction parameters | |
| Re | : | Reynolds number |
| : | Constant parameter | |
| N | : | Power law index |
| Pr | : | Prandtl number |
| Sc | : | Schmidt number |
| : | Magnetic dipole | |
| : | Radius of the disc | |
| : | Feature radius | |
| : | Brownian diffusion | |
| : | Thermophoresis diffusion | |
| M | : | Variation of magnetization |
| : | Curie temperature | |
| T | : | Temperature |
| : | Yield stress of fluid | |
| Br | : | Brinkman number |
| : | Radiation parameter | |
| : | Temperature ratio parameter | |
| Ha | : | Hartmann number |
| Ec | : | Eckert number |
| Nt | : | Thermophoresis |
| Nb | : | Brownian motion |
| : | Chemical reaction parameter | |
| K | : | Porosity parameter |
| OHAM | : | Optimal Homotopy Analysis Method |
| FHD | : | Ferro hydrodynamic parameter |
| BCs | : | Boundary Conditions |
Greek Symbols
| : | Dimensionless thickness co-efficient of the disc | |
| : | Fluid density | |
| : | Produced by combining a component of deformation with itself | |
| : | Casson parameter | |
| : | Critical value of this product | |
| : | Plastic dynamic viscosity |
1. Introduction
In recent era, studies on nanofluids are receiving a lot of attention from academics every day as a result of its large and widespread applications in modern technology and for facilitating a variety of industries such as the phenomenon of heat transfer. Some applications of nanofluid are the thermal insulating, atomic rotators, chemotherapy for cancer, electronic apparatuses, nuclear reactor cooling, systems for converting energy, energy production and artificial heart surgery. The initial research was done by Choi,1 who also presented empirical data to back up the idea that the appropriate collisions of nano crystals might improve the thermal properties of base fluids. Choi invented the term nanofluid initially. Later, Buongiorno2 proposed a nanofluid model that took into consideration of Brownian movement and thermophoresis effects to characterize the heat and mass transfer. Rehmann et al.3 discussed the MHD Casson nanofluid flow with the presence of uniform magnetic field, heat generation, chemical reaction and they applied R-K-F method to report the heat transfer aspects with different combinations of nanofluid parameters. MHD mixed nanofluid flow over the rotating disc with the presence of boundary condition of third kind, magnetic field and heat generation effect is reported by Prasad et al.4 and they adopted OHAM to analyze the aspects of heat and mass transfer. Shaw et al.5 deliberated the Darcy–Forchheimer -Casson/Water nanofluid flow over the rotating disc and entropy generation, nonlinear thermal radiation are considered. To analyze the heat and mass transport phenomenon, they employed R-K method with shooting technique. Ramzan et al.6 studied the effect of auto catalytic chemical reaction and heterogeneous reaction across a porous disc. They utilized variable thermal properties to analyze the heat transfer aspects over the disc. Consequences of Local Thermal Nonequilibrium and passive control approach over the rotating porous disc are studied by Ragupathi et al.7 They adopted three temperature models to determine the heat and mass transfer aspects of the Ostwald de Wale nanofluid. Subsequently, numerous researchers have published a variety of conclusions after taking into account distinct kinds of nanofluid.
Moreover, Ferrofluid flow is a fascinating research area since it has the potential to be used in rotating shaft sealing, efficient electrical motors and spin coating. Most commonly referred to as magnetic nanofluid is ferrofluid (MNF) and magnetic nanoparticles of Fe, Co, and are suspended colloidally in the base liquid. Ganguly et al.8 used explicit finite difference method to examine the magnetic fluid flow over the small channel. They also came to the conclusion that increasing the magnetic dipoles in the channel improves heat transfer rates. Consequences of magnetic dipole on the rotating cylinder in the channel are reported by Selimefendigil and Oztop9 and they reported the heat transfer aspects of the cylinder in the channel when the cylinder rotates in clockwise. Zeeshan et al.10 explored the impact of magnetic dipole viscous ferro-fluid over the stretching surface. They adopted the Runge–Kutta method to analyze the hydrodynamic and heat transfer aspects. Majeed et al.11 discussed the visco-elastic fluid flow across a stretching sheet with the occurrence of the suction effect. Flow of dual stratified Casson fluid flow over the stretching sheet with the presence of Fourier’s and Fick’s law is scrutinized by Chen et al.12 The Blasius Rayleigh Stokes flow across a moving plate with adjustable thermal conductivity and a magnetic dipole is quantitatively reported by Reddy et al.13
On the other hand, Joule heating has a number of important applications in electrical engineering, including the design of electric heaters, resistors and electric furnaces. It is also an important factor to consider in the design of electronic circuits, as it can lead to overheating and damage to components. Thermophoretic MHD Powell–Eyring fluid flow through a vertical stretching sheet with existence of chemical reaction and Joule heating is studied by Khan et al.14 and they talked numerically and analytically about the effects of different combination fluid parameters on the profiles of heat and mass transmission. Hayat et al.15 reported the fluid flow over the disc with the presence of viscous dissipation and Joule heating. Also, to examine the features of heat transfer through the disc, they used the HAM approach. Das et al.16 employed single-phase model to investigate the steady magneto hydrodynamic boundary layer flow over the infinite noncoaxial rotating disc with the presence of applied uniform magnetic field and Hall currents. The swirling flow of Maxwell fluid over the rotating porous disc is depicted by Ahmed et al.17 with the occurrence of Joule heating, and the RKF technique is used to explore the heat transmission aspects on the porous disc. Das et al.18 reported the magnetized Cu-engine oil based non-Newtonian Casson nanofluid flow over the rotating slipping porous disc with the presence of convective heating and hall effect. They concluded hall current generates a substantial enhancement in velocity component profiles and significantly elevates the temperature in the flow system. Ilyas et al.19 reported the consequences of Joule heating and viscous dissipation on the rotating disc and they adopted Levenberg–Marquardt back propagation (LMBP) scheme, hybrid hydro-nanofluid model to explore the heat transfer aspects over the disc. Hafeez et al.20 adopted Cattaneo–Christov double diffusion theory and non-Newtonian Oldroyd-B nanofluid flow over spinning disc with the presence of Joule heating to analyze the hydrodynamic and heat transfer characteristics.
Researchers are paying a lot of attention to the thermal radiation because it has a wide range of physical, engineering and industrial applications such as glass production, polymer processing, space technologies like missiles and rockets, as well as missiles, rockets and power plants. Shehzad et al.21 investigated the thermal radiated three Jeffrey nanofluid flow over the stretching surface. Impact of heat source sink and radiation effect over the inclined magnetic stretching sheet is examined analytically by Hayat et al.22 Khan et al.23 used Magneto-Burgers bio-nanofluid of mixed convection flow over the vertical plate to examine the hydro-dynamic and heat transfer aspects. Jyothi et al.24 perceived the influence of radiation effect and partial slip conditions on Carreau nanofluid flow over a wedge and they found the heat and mass transport rate is significantly affected by the radiation and slip effect. Moreover, impact of radiative hybrid nanofluid flow over the rotating disc with Hall effect is reported by Acharya et al.25 Abbasi et al.26 discussed the importance of activation energy, SWCNT and MWCNT on the nonlinear radiated rotational stagnation point hybrid nanofluid flow over the disc. The optimized flow of second-grade nanofluid flow over the disc with nonlinear thermal radiation is reported by Alsallami et al.27
Entropy analysis is an essential tool in the field of thermodynamics and energy engineering that is used to evaluate the thermodynamic performance of a system. It involves analyzing the amount of entropy generated in a system during a thermodynamic process and can be used to determine the efficiency of a system, as well as identify areas of energy loss and potential improvements. In general, entropy is a measure of the degree of disorder or randomness in a system and is closely related to the concept of energy. Entropy analysis is often used to design and optimize energy systems such as power plants, refrigeration and air conditioning systems and engines. By analyzing the amount of entropy generated during the operation of these systems, engineers and scientists can identify ways to increase the system’s efficiency and reduce energy losses. Arikoglu et al.28 presented the analysis of second law of thermodynamics with the presence of partial slip conditions. Rashidi et al.29 investigated the entropy generation rate of MHD nanofluid flow over the rotating disc with the presence of magnetic field. Hayat et al.30 discussed the entropy analysis of MHD radiative flow over the disc with the existence of Joule heating and viscous dissipation. Second grade nanofluid flow over the rotating disc is deliberated by Javed et al.31 The important finding showing the effect of entropy creation is that the entropy generation rate is slowed down by higher estimations of the Bejan number and fluid parameter. Bhandari32 examined the ferro-fluid flow over the stretchable coaxial rotating disc with the presence of magnetic dipole and Joule heating. Recently, Sutterby nanomaterials radiated flow through the rotating disc with the presence of activation energy and heat generation effect is reported by Rahman et al.33
It can be seen that not enough articles are available for the Casson nanofluid flow over the rotating porous disc. So, it encouraged us to examine the entropy analysis for the Casson nanofluid flow over the rotating porous disc with the presence of the magnetic dipole, nonlinear thermal radiation, Joule heating and viscous dissipation. The Brownian movement and thermophoresis effects are incorporated to develop the heat transfer mechanism and passive control approach is accounted in boundary condition. The Von-Karman similarity variables are used to convert the partial governing equation into ordinary differential equations (ODEs). The HAM approach is employed to solve the mathematical model. The entropy generation, hydrodynamic, heat and mass transport aspects are reviewed via the graphical illustration. Also, the skin friction, heat and mass transfer rates are discussed with help of the tables. Moreover, Casson nanofluid flow through the rotating disc is widely recognized due to its many applications such as the design of turbines, oil and gas drilling, MHD generators, food processing, printing industry, drug delivery, tissue engineering, coatings and paints.
2. Mathematical Description of the System
Consider the viscous fluid flow over the rotating porous disc. The variable thickness and the radius of the porous disc is assumed as and along with the cylindrical coordinate system . The angular frequency of the porous disc is denoted by about the z-axis (see Fig. 1). Temperature maintained on the surface of the disc is taken as while temperature away from the surface of the disc is . The external uniform magnetic field is applied perpendicular to the surface of the disc and has a constant magnetic flux density which is assumed unchanging with a small magnetic Reynolds number .
Fig. 1. (Color online) Physical configuration.
2.1. Conditions and assumptions of the model
The following conditions and assumptions are considered in the modeling:
| • | Time-independent incompressible Casson fluid flow model is considered. | ||||
| • | Joule heating and magnetic dipole are employed to simulate the fluid flow system. | ||||
| • | Nonlinear thermal radiation, viscous dissipation, thermophoresis and Brownian motion are considered to develop the heat transfer mechanism. | ||||
| • | Chemical reaction effect is considered to develop the mass transfer mechanism. | ||||
| • | Passive control approach is accounted at the boundary condition. | ||||
| • | Rotating porous disc. | ||||
2.2. Casson fluid model
For an incompressible Casson nanofluid, the rheological equation of state can be expressed as follows4 :
2.3. Modeling
Using the above aforementioned suppositions, the governing PDEs are given as follows6,7 :
2.4. Magnetic dipole
The mathematical definition of the magnetic scalar potential with magnetic dipole () is
Taking into account insignificant fluctuation along the z-axis, the associated magnetic field H has the following components :
The mathematical statement in magnitude form, where H is the magnetic field, has an insignificant fluctuation in the z-direction in this case.
It is considered that the generalized linear magnetic equation of state is ; for the Casson nanofluid’s saturation and the relationship between the magnetization M and temperature, where K stands for Pyro-magnetic co-efficient.
2.5. Similarity variables
The Von-Karman similarity variable is defined as follows6,7 :
Equations (2)–(6) with the BCs (7) are reduced to
Equations (12)–(17) are modified into
3. Physical Quantities
3.1. Skin friction
The tangential and radial shear stresses on the disc’s surface are as follows :
The form of the drag coefficient is as follows :
3.2. Nusselt number
The wall heat flux at surface of the disc is
3.3. Sherwood number
The mass transfer rate can be expressed as follows :
4. Entropy Generation
The local entropy generation of the present problem is
The entropy generation rate NG becomes
5. Method of Solution
In the math world, the Homotopy Analysis Method (HAM) is a powerful method to solve the nonlinear differential equations. It was introduced by Prof. Liao in 1992 and has since gained widespread attention in the scientific community due to its simplicity, efficiency and accuracy. The basic idea behind the HAM is to transform a nonlinear differential equation into a series of linear equations, which can then be solved iteratively. The iterative process involves introducing a parameter called the homotopy parameter, which transforms the original equation into a series of equations with varying degrees of nonlinearity. As the value of the homotopy parameter changes, the solution of the equation evolves from the initial guess to the exact solution. One of the key advantages of the HAM is that it does not require any restrictive assumptions or approximations, unlike other methods such as perturbation methods or numerical methods. It can be applied to a wide range of nonlinear problems in various fields, including physics, engineering, biology and finance.
By following the procedure of HAM, the following are the early guesses :
5.1. Zeroth-order deformation
Let us consider the embedding parameter in the HAM approach as and and are the auxiliary parameters and it never vanish.
The zeroth-order deformation becomes
5.2. nth-order deformation problem
According to this formulation, the problem at nth order is described as follows :
The general solution of Eqs. (46)–(50) becomes
Convergence analysis
In HAM technique, the value of the auxiliary parameter determines the solution’s convergence rate. The -curve is depicted here at the 20th order of approximation. Plotting h-curves yields valid ranges for these parameters (see Fig. 2). The acceptable ranges for , , , and are , , , and . Table 1 shows the comparison findings, which are in great agreement.
| Authors | ||
|---|---|---|
| Ramzan et al.6 | 0.510210 | 0.615921 |
| Ragupathi et al.7 | 0.510232 | 0.615921 |
| Acharya et al.25 | 0.510231 | 0.615921 |
| Present | 0.510223 | 0.615882 |
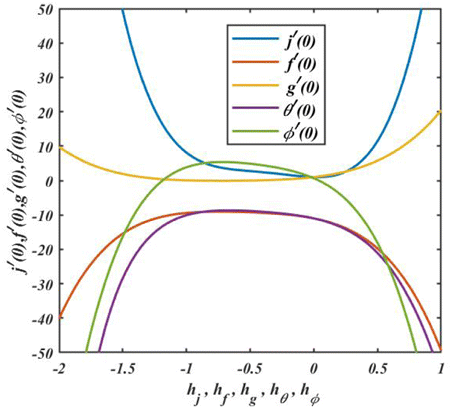
Fig. 2. (Color online) curve for , , , and .
6. Results and Discussion
The consequences of the Casson nanofluid flow across a rotating disc with the presence of magnetic dipole, nonlinear thermal radiation, Joule heating and viscous dissipation are covered in this section. Graphical representations are used to explain entropy generation rate (NG), heat and mass transport aspects. To achieve the desired results, the physical parametric variables are set to , , , , , , , , , , and . Furthermore, tables have been used to investigate drag coefficient, heat and mass transfer rates.
6.1. Hydrodynamic aspects
The impact of Ha on the radial and tangential velocities is sketched in Fig. 3. Physically, at low Hartmann numbers (Ha), the viscous forces dominate over the electromagnetic forces, and the fluid velocity is not significantly affected by the magnetic field. However, as the Hartmann number increases, the electromagnetic forces become stronger and can suppress the fluid velocity. Therefore, the fluid velocity is diminished due to increasing the values of Ha, which are illustrated in Fig. 3. Effect of porosity parameter on the and is shown in Fig. 4. It is clearly noted that the radial and tangential velocity is lowered when upsurging the values of K. The reason is the presence of pores in a porous medium creates resistance to fluid flow, which reduces the fluid’s velocity. The magnitude of this reduction in velocity depends on the porosity of the medium, as well as other factors such as the viscosity and density of the fluid. Thus, decreasing the fluid velocity.
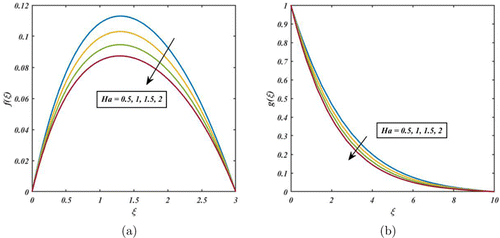
Fig. 3. (Color online) Impact of Hartmann number on the and .
Fig. 4. (Color online) Impact of K on and .
Figure 5 characterizes the consequences of Casson parameter on the radial and tangential velocity. Based on the graphical depiction, the tangential velocity is decayed by increasing the values of (see Fig. 5(b)). In fact, higher Casson parameter for a given flow rate will lead to higher yield stress and more significant resistance to flow. This means that the velocity field will be lower in regions where the fluid experiences higher shear stress or resistance to flow. But, the opposite tendency is shown in Fig. 5(a) for the radial velocity. Effect of FHD parameter on the radial and tangential velocities is highlighted in Fig. 6. When the FHD parameter is high, the magnetic forces on the nanofluid particles are strong, leading to a more significant deformation of the fluid and a higher velocity field. As a result, the radial velocity of the fluid enhances. On the other hand, opposite trend is observed in the tangential velocity (see Fig. 6(b)).
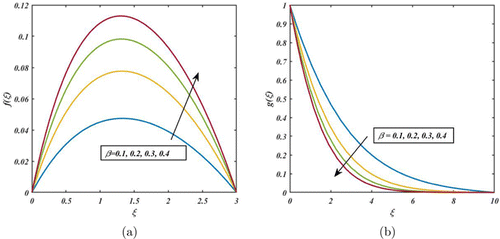
Fig. 5. (Color online) Impact of on and .
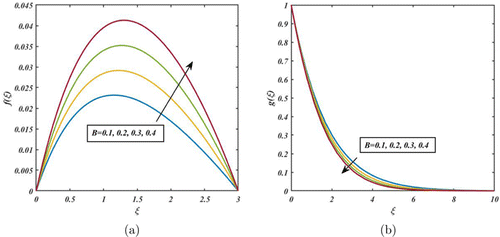
Fig. 6. (Color online) Impact of B on and .
6.2. Heat transfer aspects
The contribution of and on is portrayed in Figs. 7(a) and 7(b). The heat transfer profile is decayed by enhancing the values of FHD parameter . In the energy equation, the FHD interaction parameter is high, the magnetic torque is strong, and the fluid flow is also strong, resulting in a high heat dissipation rate and significantly affecting the temperature field. Thus, the fluid temperature reduces. Figure 7(c) describes the effect of Ha on the heat transfer profile. Due to the increase in Ha values, the heat transfer profile is escalated. When the Hartmann number is high (i.e., when the magnetic field is strong compared to the viscous forces), it can suppress fluid motion and therefore decrease the rate of heat transfer. This is because the magnetic field acts to oppose the fluid motion and reduces the turbulence in the fluid. As a result, the temperature field can become more uniform, with less variation in temperature across the fluid. Impact of Ec on the heat transfer profile is depicted in Fig. 7(d). Physically, a higher Eckert number means that the kinetic energy of the flow is more dominant compared to the enthalpy, and therefore, the temperature rise due to frictional heating is relatively small. Thus, the temperature of the fluid system increases.
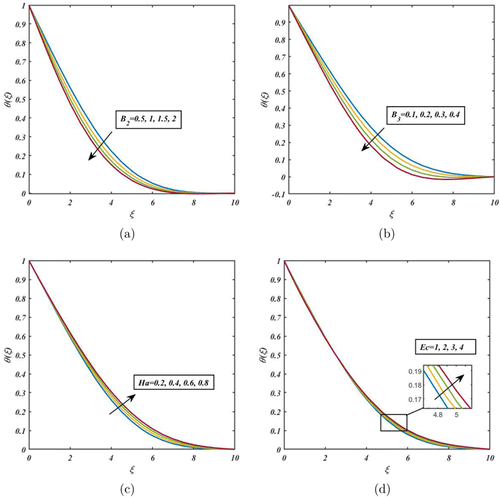
Fig. 7. (Color online) Impact of , , Ha, Ec on .
Figure 8(a) shows the impact of Nt on the heat transfer profile. From the pictorial representation, the temperature profile is enhanced by increasing the values of thermophoresis parameter Nt. Generally, thermophoresis is a phenomenon that occurs when particles in a fluid move in response to a temperature gradient. In thermophoresis, particles experience a force that causes them to move from high-temperature regions to low-temperature regions and this force is proportional to the temperature gradient. This increases the thermal layer thickness. Impact of Pr on the thermal profile is demonstrated in Fig. 8(b). It is observed that increases in the values of Pr cause a decrease in temperature. In terms of physics, thermal diffusivity affects the Pr. A weaker thermal diffusivity is associated with higher values of the Pr. Such a decreased thermal diffusivity causes a decrease in the temperature profile and the accompanying thermal layer thickness. The fluctuation of the over the energy field is depicted in Fig. 8(c). It has been shown that the temperature profile is escalated due to increasing the values of . This is because a higher radiation parameter means that the porous surface can emit more energy through radiation. In contrast, an importance of on the energy filed is demonstrated in Fig. 8(d). By using greater values of , the temperature field and thickness of the thermal layers are raised. Because of this, the ambient temperature is lower than the temperature of the walls.
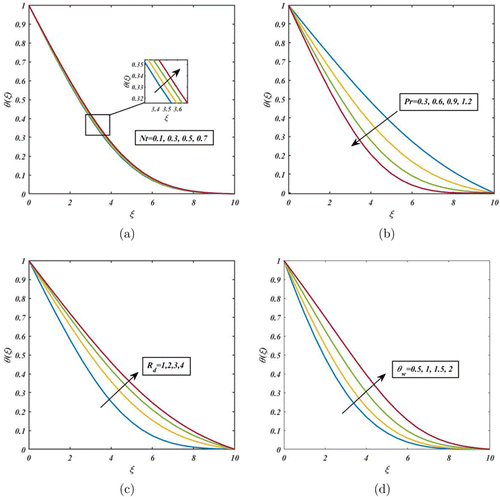
Fig. 8. (Color online) Impact of Nt, Pr, , on .
6.3. Mass transfer aspects
Figure 9(a) shows the impact of Nt on the volumetric concentration. It is clearly noted that the volumetric concentration has been decreased near the disc’s surface due to increase in the values of Nt. The nano crystals move from hot to colder regions because of the temperature gradient. As a result, the concentration profile diminished by increasing the thermophoretic force. Figure 9(b) reveals the consequences of Nb against the mass transfer. For higher values of the Brownian motion (Nb), the mass transfer and associated layer thickness are increased near the disc’s surface. Figures 9(c) and 9(d) illustrate the effects of and Sc on the concentration profile. It is observed from Fig. 9(c) that the volumetric concentration is enhanced due to accelerating the values of . From Fig. 9(d), when the values of Sc escalate, the volumetric concentration profile increased. In general, a higher Schmidt number indicates a greater resistance to mass transfer due to the slower rate of diffusion.
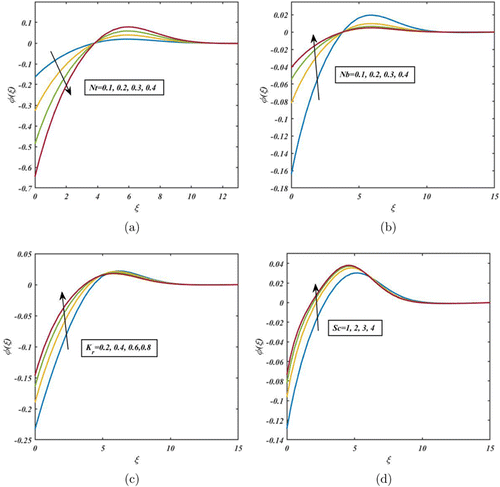
Fig. 9. (Color online) Impact of Nt, Nb, , Sc on .
6.4. Entropy generation and Bejan number
Figures 10–12 demonstrate the impact of FHD interaction parameters on Be and NG. When the FHD interaction parameter is high, the magnetic interactions between the nanoparticles are strong, and the particles tend to move together more coherently. This results in a more ordered flow and higher energy dissipation due to magnetic interactions, generating higher NG. On the other hand, opposite tendency is observed in the case of Be (see Fig. 10(a)). Consequently, a similar manner is noted in the other FHD parameters such as (see Figs. 11 and 12). The fluctuation of Ha on Be and NG is depicted in Fig. 13. From Fig. 13(a), Be decreases as Ha increases near the disc’s surface because viscous dissipation irreversibility predominates over the heat transfer irreversibility. Furthermore, from Fig. 13(b), the NG rate is significantly affected away from the disc’s surface by increasing the values of Ha. When the Ha is large, the magnetic field is strong, and the fluid flow becomes more laminar and less turbulent. This reduces the level of mixing and increases the efficiency of the fluid system, which can lead to a decrease in NG.
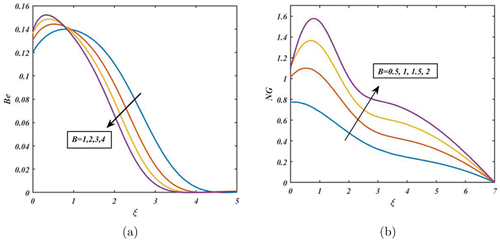
Fig. 10. (Color online) Impact of B on Be and NG.
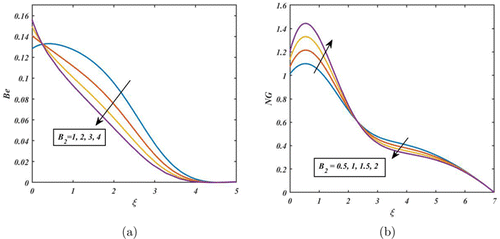
Fig. 11. (Color online) Impact of on Be and NG.
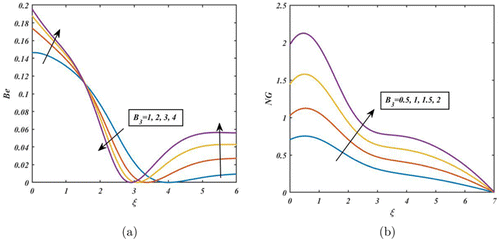
Fig. 12. (Color online) Impact of on Be and NG.
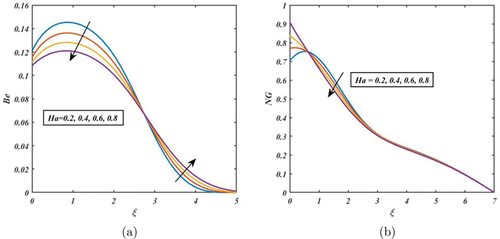
Fig. 13. (Color online) Impact of Ha on Be and NG.
As depicted in Fig. 14(b), NG grows as Ec increases since that relevant heat is a type of disordered energy (energy with less quality and more entropy). The significance of Ec on NG in fluid flows is that a higher Ec leads to a higher rate of entropy generation, since more thermal energy is being converted into mechanical energy. Therefore, the NG rate consequently rises. On the contrary, the impact of Ec on Be is as shown in Fig. 14(a). Be increases with an increase in Ec values. Furthermore, approximately it reaches its peak value in . After that, the Be rate is gradually decreased due to enhancing the value of Ec. Figure 15(b) shows the enhancement in the degree of the disorder by escalating Br for NG. Physically, heat is transported by nanoparticles, and viscous dissipation prevails the entire process. Increasing Br results in more viscous heating compared to conductive heat transfer, which generates more heat. It disturbs the entire fluid system and generates a lot of heat between the layers of the moving fluid. Therefore, the NG process is directly impacted by Br. Resulting, the NG rate enhances. On the other hand, it can be seen from Fig. 15(a) that the Be rate is affected significantly by enhancing the values of Br.
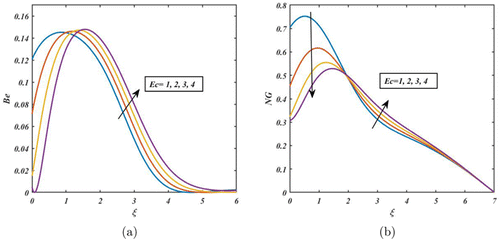
Fig. 14. (Color online) Impact of Ec on Be and NG.
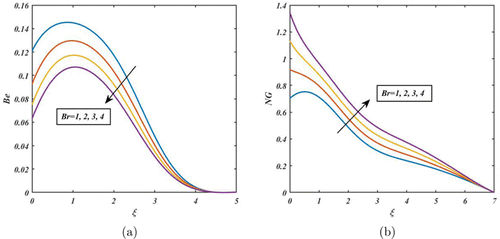
Fig. 15. (Color online) Impact of Br on Be and NG.
From Fig. 16, by increasing the values of , NG and Be are enhanced. In fact, the fluid flow system gains more internal energy. Due to this, both the Be and NG rates rise. In contrast, the fluid flow system is slowed down by increasing the values of Re. At high Re, the inertial forces dominate the fluid flow and the viscous dissipation of energy is low. In this case, the entropy generation due to viscous dissipation is also low (see Fig. 17(b)). From Fig. 17(a), Be is enhanced due to upsurging the values of Re. This is because heat transfer effects prevail over magnetic fields and fluid friction at higher Re. Figure 18 indicates the NG rate and Be are increased due to enhancing . affects the rate of heat transfer between the system and the surroundings, which in turn affects the rate of NG. The temperature ratio is high, there is a large temperature difference between the system and the surroundings, and the rate of heat transfer is high. This leads to a higher rate of NG and Be. Figure 19 reveals how the Casson parameter affects Be and NG. Be is enhanced near the disc’s surface by accelerating the values of Casson parameter and diminished away from the disc’s surface. Moreover, the total (NG) rate is accelerated due to increasing Casson parameter (see Fig. 19(b)). The Casson parameter can affect NG in a fluid flow system by influencing the shear stresses and viscosity gradients in the fluid. Specifically, a higher Casson parameter (indicating a higher yield stress and more shear-thickening behavior) can lead to higher shear stresses and viscosity gradients, which in turn can result in higher levels of NG.
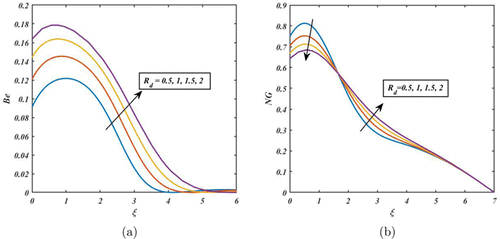
Fig. 16. (Color online) Impact of on Be and NG.
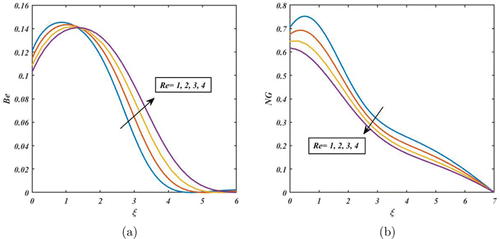
Fig. 17. (Color online) Impact of Re on Be and NG.
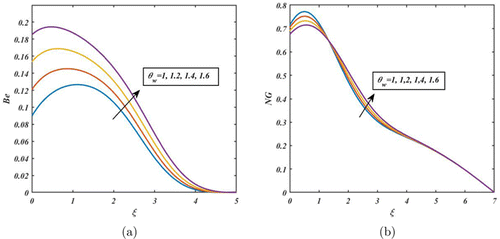
Fig. 18. (Color online) Impact of on Be and NG.
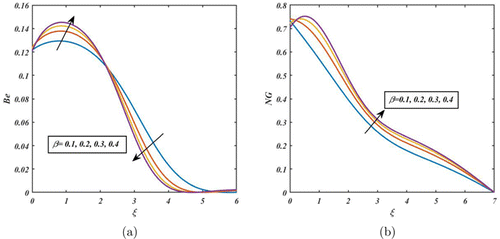
Fig. 19. (Color online) Impact of on Be and NG.
6.5. Analysis of tables
Table 2 provides the numerical information about the skin friction coefficient. Table 1 indicates that the skin friction rate is increased due to enhancing the values of FHD parameter . But, the opposite behavior is noticed in the scenario of lower values of Ha, Re, K and . The heat transfer rate is reported in Table 3 for various combinations of nanofluid parameters. Due to increasing amount of Radiation, Eckert and Prandtl number the heat transfer is enhanced. But in the instance of the heat transfer rate is diminished when increasing the values of FHD and thermophoresis parameters. Table 4 indicates the mass transfer rate. The mass transfer rate is declined due to upswing in the values of Sc, Nb, Kr. But, the reverse tendency is received in the case of the higher value of thermophoresis.
| Ha | B | Re | K | ||
|---|---|---|---|---|---|
| 0.5 | 0.2 | 1 | 0.3 | 0.5 | 2.11581628086132 |
| 1 | 2.10518966285625 | ||||
| 1.5 | 2.09865246649875 | ||||
| 0.4 | 2.14769081297266 | ||||
| 0.6 | 2.18661154064418 | ||||
| 0.8 | 2.23163201605066 | ||||
| 2 | 2.10730735313949 | ||||
| 3 | 2.09331867274338 | ||||
| 4 | 2.08889077251765 | ||||
| 0.3 | 2.12197063421876 | ||||
| 0.6 | 2.11321916941696 | ||||
| 0.9 | 2.10690176126541 | ||||
| 0.1 | 7.65231835769864 | ||||
| 0.2 | 4.19609313927657 | ||||
| 0.3 | 3.04387633600344 |
| R | Ha | Ec | Nb | Nt | Pr | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 0.2 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.5 | 0.306427054800514 |
| 2 | 0.342599699314200 | ||||||||
| 3 | 0.380601446415209 | ||||||||
| 0.5 | 0.301010112823726 | ||||||||
| 1 | 0.295980501142645 | ||||||||
| 1.5 | 0.294663098413244 | ||||||||
| 0.4 | 0.302107136165326 | ||||||||
| 0.8 | 0.304260670906245 | ||||||||
| 1.2 | 0.306359002159087 | ||||||||
| 0.3 | 0.322614428070648 | ||||||||
| 0.6 | 0.352240578247521 | ||||||||
| 0.9 | 0.379150931742468 | ||||||||
| 0.3 | 0.351636591762454 | ||||||||
| 0.6 | 0.423016613705286 | ||||||||
| 0.9 | 0.489411362137901 | ||||||||
| 0.2 | 0.301010112823726 | ||||||||
| 0.4 | 0.343695723787405 | ||||||||
| 0.6 | 0.375312604190891 | ||||||||
| 0.2 | 0.301010112823726 | ||||||||
| 0.4 | 0.301010122083775 | ||||||||
| 0.6 | 0.301010157234299 | ||||||||
| 0.2 | 0.301010112823726 | ||||||||
| 0.4 | 0.292911733553312 | ||||||||
| 0.6 | 0.285012003370576 | ||||||||
| 1 | 0.400077798403161 | ||||||||
| 2 | 0.520666490198168 | ||||||||
| 3 | 0.599227235510901 |
| Sc | Nb | Nt | Kr | |
|---|---|---|---|---|
| 0.6 | 0.2 | 0.2 | 0.5 | 0.603515774634799 |
| 1.2 | 0.583360603285077 | |||
| 1.8 | 0.571223073291250 | |||
| 0.6 | 0.4 | 0.2 | 0.5 | 0.301757886485771 |
| 0.6 | 0.201171907000352 | |||
| 0.8 | 0.150878930250241 | |||
| 0.6 | 0.2 | 0.4 | 0.5 | 1.185683729642290 |
| 0.6 | 1.746039247836860 | |||
| 0.8 | 2.284412862669180 | |||
| 0.6 | 0.2 | 0.2 | 1 | 0.592634951905500 |
| 2 | 0.581122889024938 | |||
| 3 | 0.574446465981997 |
7. Conclusion
In this work, the Casson nanofluid flow over the rotating disc in the presence of the magnetic dipole, viscous dissipation, Joule heating, chemical reaction and nonlinear thermal radiation is examined. By employing Von-Karman similarity variables, the system of PDEs are transformed into a system of ODEs, and the highly nonlinear ODEs are resolved by the HAM. The most pertinent nondimensional parameters on the velocity, heat and mass transfer and entropy rate are analyzed via graphical representation. In addition, the drag co-efficient, heat and mass transfer rates are discussed with help of the tables. The following results are the crucial findings in this work:
| • | Both radial and tangential velocity profiles are diminished by enhancing the values of Hartmann number (Ha). This is because the electromagnetic forces dominate over viscous forces. | ||||
| • | By increasing the value of Casson parameter , the flow rate enhances the yield stress. Thus decreasing the radial velocity of the bio-nanofluid. Also, the reverse trend is attained in the tangential velocity. | ||||
| • | When enhancing the FHD parameter values, the temperature profile diminishes. The reason for this phenomenon is the high viscosity dissipation. | ||||
| • | The temperature profile is enhanced due to upsurging Eckert number (Ec) values. This is because the frictional heating between the layers is small, which enhances the temperature profile. | ||||
| • | When the radiation parameter escalates, the porous surface emits more energy through the radiation phenomenon. Therefore, the temperature profile accelerates. | ||||
| • | The volumetric profile is decayed due to enhancing the values of thermophoretic value (Nt). While the opposite behavior is observed when improving the values of Brownian motion (Nb). | ||||
| • | A higher value of Eckert number (Ec) increases the entropy generation rate. In this process, more thermal energy is converted into mechanical energy. | ||||
| • | The entropy generation rate is accelerated due to increase in the Brinkman number (Br) values since the viscous dissipation effect is more compared to conductive heat, which generates more heat. Thus improved the entropy rate of the entire fluid system. | ||||
| • | By enhancing the thermal radiation parameter both entropy and Bejan number rate are enhanced because the fluid system gains more internal energy when improving the radiation value. | ||||
| You currently do not have access to the full text article. |
|---|


