A Tumor-Immune System with Switching Threshold Depending on Tumor Cells and Its Change Rate
Abstract
Tumor prevention and control, taking into account the load of tumor cells or immune cells, are often described by Filippov systems, usually with a smooth function on the right-hand side describing the tumor immunity. However, these systems only consider the load of tumor cells or immune cells as a threshold function, which suggest that patients will only be treated if the load of tumor cells or immune cells exceeds a certain threshold. As a result, there may be an excessive growth of tumor cells or a rapid decrease in immune cells, which can lead to undesirable results. Considering this problem, we propose a weighted switching system using the load of tumor cells and its change rate as the threshold. Theoretical analysis and numerical simulation of the system are performed by changing the threshold value. We find that in the proposed nonlinear weighted threshold control method for the system, on the one hand, the system can produce rich dynamical behaviors, including many possible cases of bistability and sliding segments of the system, etc., and on the other hand, it is also very important for the prevention and control of tumor.
1. Introduction
Tumor is a significant disease affecting human health and one of the leading causes of death in humans [Farayola et al., 2020]. It is worthwhile to pay attention to the prevention and treatment of tumor in the early stage, which is not only the most vulnerable stage of tumor, but also the stage that can be easily ignored. In the process of advancing medical standards and technology, in addition to traditional surgery, radiotherapy and chemotherapy, targeted therapy and immunotherapy are gradually coming into people’s view [Mantovani et al., 2008; Leschiera et al., 2022]. The difference between immunotherapy and conventional treatment is that immunotherapy mobilizes the patient’s own immune anti-tumor ability, so once the efficacy is obtained, it lasts for a longer and more durable period of time. It also improves the patient’s immune function which has been damaged by radiotherapy, so it has the complementary advantages of the combination of three conventional therapies [Hervault & Thanh, 2014; Yu & Jang, 2019; Robertson-Tessi et al., 2012; Ledzewicz et al., 2012]. For example, by combining immunotherapy and chemotherapy and by injecting patients at different time intervals, the effect of reducing the side effects of drugs on patients and improving the efficiency of treatment can be achieved [Hervault & Thanh, 2014; Ledzewicz et al., 2012; Novoselova et al., 2019]. The combination of immunotherapy and radiotherapy is still controversial, mainly because there is no optimal method to combine radiotherapy with immunotherapy, and there are still many unresolved issues in terms of dosage, treatment techniques, duration, and safety. However, the combination of immunotherapy and radiotherapy has great potential and advantages and is still undergoing extensive clinical trials [Kang et al., 2016; Yu et al., 2019]. In addition, there are many mechanisms and evidence suggesting that surgical resection of primary tumor affects the patient’s immune system, and that post-surgery-induced immunosuppression reduces the likelihood of metastatic diseases. From this perspective, the combination of immunotherapy and surgery remains promising [Tai et al., 2013; Yakar et al., 2003].
In recent years, researchers have investigated the interrelationship with tumor cells and immune cells by establishing and analyzing a nonsmooth dynamic model [Hou et al., 2022]. On the one hand, the relationship is analogous to that of “predator and prey”; on the other hand, their relationship is “competitive”. There is no clear and unambiguous definition of the correlation of tumor and the immune system, as it involves multiple factors and mechanisms. This is a complex and diverse area of research, and scholars are constantly striving to deepen their understanding of tumor immunology. For different types of tumor and different individuals, there may be differences in the manner and outcome of tumor-immune system interactions. This also makes accurate definitions difficult to generalize [Ali et al., 2019].
In addition, other studies have described mathematical models by introducing Filippov systems with thresholds that fully account for the effect on the model when the tumor cell load is above the threshold function or when the immune cell load is below the threshold function [Tang et al., 2017a], but do not include the rate of change of the tumor cells or the immune cells themselves. Immunotherapy is only administered when the load of tumor cells is above a certain threshold level or when the load of immune cells is below a certain level threshold. This may lead to a situation where even if the rate of change of tumor cells increases, as long as the load of tumor cells does not exceed a certain threshold, the patient will not receive immunotherapy. Or perhaps the rate of change of immune cells decreases, but the load of immune cells is not reduced to a certain threshold, and no preventive or control measures will be taken for the patient. Both of these may lead to the tumor progressing to an uncontrollable stage [Jang & Yu, 2009; Ren et al., 2022].
On this basis, a nonlinear threshold function is proposed by incorporating the Filippov tumor-immune model, considering the load of tumor cells and its change rate. We assign certain weights to the model, and only when the weights of the load of tumor cells and its change rate add up to a certain threshold, the patient can receive immunotherapy and other means. When the tumor cell load is below the threshold value, we assume that the patient’s own immune cells are sufficient to control tumor growth. The proposed nonsmooth Filippov tumor-immune model is as follows:
The boundary conditions need to consider the sum of the proportions of the tumor cells and its change rate. Assume that H(X)=a1y1+a2ẏ1|S1−ET where ẏ1|S1 represents the differential equation for the load of tumor cells in the subsystem S1 (a detailed explanation of the threshold function H(X) will be presented in Sec. 2). Thus, the boundary of the Filippov system (1) is defined as ∑:={X∈R2+|H(X)=0}, where ET is the threshold value and a1+a2=1. A more detailed explanation is that when H(X)<0, τ=0; when H(X)>0, τ=1.
The aim of this study is to come up with a nonlinear threshold control system which describes a mathematical model of immunotherapy and which tests the effectiveness of this therapy in controlling the growth of tumor cells and keeping immune cells above a given threshold. The specific organization of this paper is given as follows. In Sec. 2, we will give some elementary definitions and preparations of the Filippov system for the next analysis of the behavior of the two subsystem dynamics. After that, we talk about the equilibrium points and their stability in Sec. 3, and analyze the sliding domain and sliding dynamics of the system in Sec. 4. The study of the global dynamics of the system will be organized in Sec. 5. The boundary equilibrium bifurcation will be discussed in Sec. 6. Last, we provide a discussion of the biological significance and give some concluding remarks in Sec. 7.
2. Elementary Definition
For simplicity, the model (1) is infinitely toughened, where
Let
Definition 2.1. If X∗ denotes a real equilibrium point, one of the following conditions is satisfied: (i) FS1(X∗)=0,H(X∗)<0; (ii) FS2(X∗)=0, H(X∗)>0.
Definition 2.2. If X∗ denotes a virtual equilibrium point, one of the following conditions is satisfied: (i) FS1(X∗)=0,H(X∗)>0; (ii) FS2(X∗)=0,H(X∗)<0.
Definition 2.3. If the equilibrium X∗ is a pseudo-equilibrium point on the sliding mode of system (3), it needs to satisfy g(x,y)=λFS1(X∗)+1−λFS2(X∗)=0, H(X∗)=0 and 0<λ<1 with λ=〈HX(X),FS2(X∗)〉〈HX(X),FS2(X∗)−FS1(X∗)〉.
Definition 2.4. If X∗ denotes the boundary equilibrium of system (3), then it is necessary to satisfy FS1(X∗)=0 or FS2(X∗)=0 with X∗∈∑s.
Definition 2.5. If X∗ denotes a tangent point of system (3), one of the following conditions is satisfied: 〈HX(X),FS1(X∗)〉=0 or 〈HX(X),FS2(X∗)〉=0 with X∗∈∑s.
3. Model Preparation and Equilibrium Points
3.1. Boundedness of solutions
Theorem 1. System (3) is bounded.
Proof. For the subsystem S1, this is true for any x>0,y≥0, according to the second equation for subsystem S1,
Hence, when t>t1, according to the first equation for subsystem S1,
3.2. Dynamics of two subsystems
For subsystem S1, there are three equilibrium points, the disease-free equilibrium point E10=(0,s) and two endemic equilibrium points E11=(x11,y11),E12=(x12,y12), in which
| (1) | In the event that det(E1i)>0,tr(E1i)<0, the equilibrium point E1i is a stable focus or node. | ||||
| (2) | In the event that det(E1i)>0,tr(E1i)>0, the equilibrium point E1i is an unstable focus or node. | ||||
| (3) | In the event that det(E1i)<0, the equilibrium point E1i is a saddle point. | ||||
For subsystem S2, there are three equilibrium points, the disease-free equilibrium point E20=(0,s) and two endemic equilibrium points E21=(x21,y21),E22=(x22,y22), where
| (1) | In the event that det(E2i)>0,tr(E2i)<0, the equilibrium point E2i is a stable focus or node. | ||||
| (2) | In the event that det(E2i)>0,tr(E2i)>0, the equilibrium point E2i is an unstable focus or node. | ||||
| (3) | In the event that det(E2i)<0, the equilibrium point E2i is a saddle point. | ||||
4. Dynamic Properties of the Filippov Tumor-Immune System
Building on the previous discussion, further insights into the dynamics on the sliding segment ∑s can be gained. As well as how to present the boundary ∑ for the trajectory change of the Filippov system, it is worth to be noticed [Deng et al., 2021].
4.1. Sliding segments
The presence of sliding segments mean σ(X)=〈HX(X),FS1〉〈HX(X),FS2〉≤0, there are two ways to understand:
| (1) | 〈HX(X),FS1〉≥0 and 〈HX(X),FS2〉≤0. | ||||
| (2) | 〈HX(X),FS1〉≤0 and 〈HX(X),FS2〉≥0. | ||||
Since H(X)=a1y+a2ẏ|S1−ET=a1y+a2(ry(1−y)−αxy)−ET, HX(X) can be characterized as
Thus,
We put
Based on the former, we can write the sliding region of the system as ∑s={(x,y)∈R2+|σ1.σ2≤0} and the crossing region of the system as ∑c={(x,y)∈R2+|σ1⋅σ2>0}. It is evident that the presence of sliding segments is associated with the positivity and negativity of the σ1 and σ2 symbols. The existence of sliding segments is discussed as follows [Deng et al., 2021, 2022].
Consider the system S1, whose tangent points are satisfied:
Similarly, consider the system S2, whose tangent points are satisfied:
In the biological sense of this paper, let’s just describe where the tangent point Tmn (m=1,2;n=1,2,3) is non-negative and assume that yTm1<yTm2<yTm3 (m=1,2) to allow further discussion. In addition, we use Tm1 for one positive intersection of σi=0 and H(X)=0; two positive intersections for Tm1 and Tm2; and three positive intersections for Tm1, Tm2, and Tm3. Then Eqs. (7) and (8) occur at most six tangent points. Due to the different positions of the two described curves σ1=0 and σ2=0, the number of tangent points of each subsystem (3) and the number of sliding segments of the system change through the threshold line H(X)=0. For convenience, let H(X)=1a2αy(−a2ry2+(a2r+a1)y−ET). Thus, we discuss the different cases where sliding segments exist as follows.
For the case where there is no sliding segment, we analyze the curve σi=0 (i=1,2) mainly in terms of the number of points at which the curve σi=0 (i=1,2) intersects H(X)=0, considering the following.
| (1) | As shown in Fig. 1(a), the threshold line H(X)=0 intersects the curve σ1=0 (red line), there is one intersection point T11, and there are one real equilibrium point E11 and one false equilibrium point E12. | ||||
| (2) | As shown in Fig. 1(b), the threshold line H(X)=0 intersects the curve σ2=0 (green line), there are two intersections T21 and T22 with two real equilibrium points E11 and E12, which are bistable phenomena. | ||||
| (3) | As shown in Figs. 1(c)–1(f), the threshold line H(X)=0 intersects the curve σi=0 (i=1,2), and there are at least three intersections T11, T21, T22 and up to six intersections T11, T12, T13, T21, T22, T23. In addition, there are two real equilibrium points E11 and E12, which are bistable phenomena. | ||||
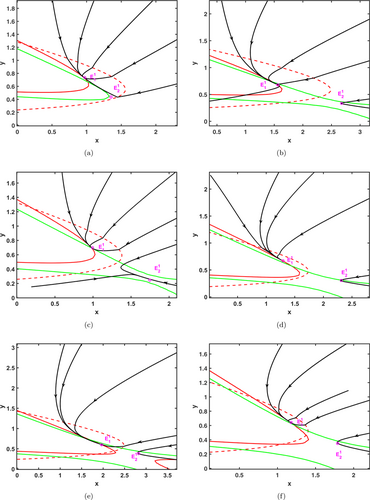
Fig. 1. The case where the sliding segment of the Filippov system does not exist. The two curves represent σ1(x)=0 (red line) and σ2(x)=0 (green line). The two points are the equilibrium points of S1 and S2, respectively. The red dashed line indicates the boundary H(X)=0. The black curve indicates the orbit on the phase plane.
For the one sliding segment, it is specifically discussed as follows [Deng et al., 2021]:
| (1) | ∑s={(x,y)|x=H(X),y∈(yT11,yT21)}, | ||||
| (2) | ∑s={(x,y)|x=H(X),y∈(yT11,yT23)}, | ||||
| (3) | ∑s={(x,y)|x=H(X),y∈(yT13,yT22)}, | ||||
| (4) | ∑s={(x,y)|x=H(X),y∈(yT22,yT12)}, | ||||
| (5) | ∑s={(x,y)|x=H(X),y∈(yT22,yT23)}, | ||||
| (6) | ∑s={(x,y)|x=H(X),y∈(yT21,yT22)}. | ||||
The six cases when there is only one sliding segment are shown in Figs. 2(a)–2(f). We can see that among the sliding segments appearing in Fig. 2(a), the two lines σ1(x)=0 (red line) and σ2(x)=0 (green line) with the threshold line H(X) appear at two tangent points with the points at the ends of the sliding segments as S1 and S2.
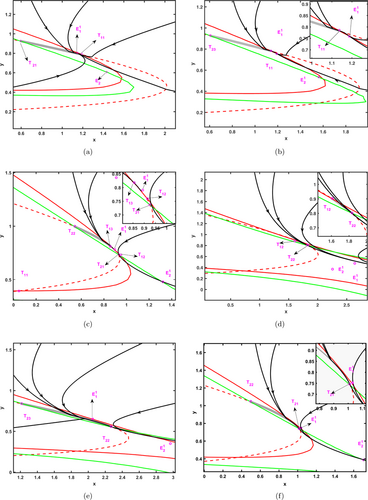
Fig. 2. Graphical representation of different cases of the existence of a sliding segment of the Filippov system. The two curves represent σ1(x)=0 (red line) and σ2(x)=0 (green line). The two points are the equilibrium points of S1 and S2, respectively. The red dashed line indicates the boundary H(X)=0 and the gray thick line indicates the sliding segment. The black curve indicates the orbit on the phase plane.
In Figs. 2(b) and 2(e), there are four intersections of the two lines σ1(x)=0 (red line) and σ2(x)=0 (green line) with the threshold line H(X), but only one sliding segment occurs, and the points at the ends of the sliding segment can be denoted, respectively, as S1 (S2) and S2 (S1).
In Fig. 2(c), there are five intersection points, but only one sliding segment occurs, and the points at the ends of the sliding segment can be denoted, respectively, as T13 and T22. There are six and four intersections of the two lines σ1(x)=0 (red line) and σ2(x)=0 (green line) with the threshold line H(X) in Figs. 2(d) and 2(f), respectively. But only one sliding segment occurs, and both the points at the ends of its sliding segment are S2.
In summary, the number of intersections of the two lines σ1(x)=0 (red line) and σ2(x)=0 (green line) with the threshold line H(X) affects the amount of tangent points and the amount of sliding segments. Also the change in parameters affects the orbits on the phase plane and also affects the number of sliding segments.
For the two sliding segments, we mainly consider the following case:
In Fig. 3, we see that the two lines σ1(x)=0 (red line) and σ2(x)=0 (green line) appear to have six intersections with the threshold line H(X), and that the points at the ends of the two sliding segments are S2 (or S1) and S1 (or S2). At this time, the equilibrium points E11 and E12 are located on the two sides of the threshold line H(X), and both are virtual equilibrium points.
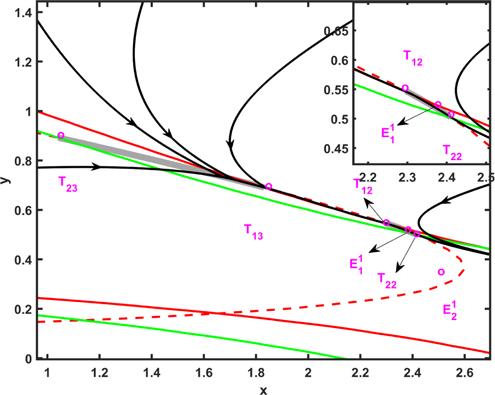
Fig. 3. Graphical representation of different cases of the existence of two sliding segments of the Filippov system. The two curves represent σ1(x)=0 (red line) and σ2(x)=0 (green line). The two points are the equilibrium points of S1 and S2, respectively. The red dashed line indicates the boundary H(X)=0 and the gray thick line indicates the sliding segment. The black curve indicates the orbit on the phase plane.
4.2. Pseudo-equilibrium
According to the previous definition,
After the calculation, we can get
For system (3), the pseudo-equilibrium point Ec=(xc,yc) satisfies the following equation:
Theorem 2. System (3) allows up to three pseudo-equilibrium points. In the presence of three pseudo-equilibrium points E1c(x1c,y1c),E2c(x2c,y2c),E3c(x3c,y3c) with E1c(x1c,y1c)<E2c(x2c,y2c)<E3c(x3c,y3c), E1c and E3c are unstable while E2c is locally stable.
Proof. Bringing H(X)=0 into (9) yields
Let f(y)=1a22y2α(a22βqry4+C3y3+C2y2+C1y−E2Tp), it goes without saying that f(0)=−E2Tp<0. Thereby, if system (3) exhibits three pseudo-equilibria E1c(x1c,y1c),E2c(x2c,y2c),E3c(x3c,y3c) with E1c(x1c,y1c)<E2c(x2c,y2c)<E3c(x3c,y3c), then there is a positive number 𝜀 such that f(y)<0 for y∈(x1c−𝜀,x1c) and f(y)>0 for y∈(x1c,x1c+𝜀). This means that dydt|∑S<0 for y∈(x1c−𝜀,x1c) and dydt|∑S>0 for y∈(x1c,x1c+𝜀). Thus, E1c is unstable. In the same way, we can see that E2c is locally stable and E3c is unstable. □
5. Global Behavior
5.1. The absence of limit cycle
In fact, considering the following section, it is essential that we must prove the absence of limit cycle. We choose the Dulac function B=1xy to define the right-hand side functions of system (4), denoted as FSi(i) (i=1,2), respectively.
For subsystem S1, there is ∂(BF(1)S1)∂x+∂(BF(2)S1)∂y=−sx2y−cx2−rx<0, therefore, the region S1 has no limit cycle.
Similarly, for subsystem S2, there is ∂(BF(1)S2)∂x+∂(BF(2)S2)∂y=−sx2y−cx2−rx<0, therefore, the region S2 has no limit cycle.
The above analysis leads to the following conclusions:
| (1) | The region Si (i=1,2) has no limit cycle. | ||||
| (2) | System (3) does not have a limit circle that contains the sliding region. | ||||
| (3) | There is no limit circle around the sliding region of system (3). | ||||
5.2. Global dynamics
We now consider the position of H(X) with respect to the endemic equilibrium point as well as focusing on the asymptotic behavior of all possible equilibria with respect to H(X), and analyze the global dynamics of the Filippov system.
Case 1. In the event that H(X) lies on the upper side of the endemic equilibrium points of subsystems S1 and S2, the endemic equilibrium point E11 is a real equilibrium and the equilibrium point E12 is a virtual equilibrium point.
In Fig. 4, we can see that all the trajectories are approaching the equilibrium point E11, meaning that the trajectories in the same region as the equilibrium point E11 go directly to the equilibrium point E11, while the trajectories in the other different regions intersect with the threshold line or converge to the equilibrium point E11 after sliding for a certain distance on the threshold line. From the previous subsection, we know that there is no limit circle in regions S1 and S2, as well as no limit circle around the sliding segment, E11 is globally asymptotically stable.
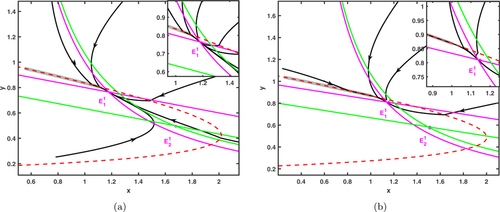
Fig. 4. Phase plane of the Filippov system of Case 1. The green and purple lines are the free system S1 and control system S2, respectively. The red line is the threshold line H(X), and the black line is the solution trajectory of system (3). The parameters of the subgraphs are denoted by (a) α=1.2, ET=0.43, a1=0.6; (b) α=1, ET=0.5, a1=0.65. The other parameters are, respectively, s=7, c=3, β=9, r=6, p=0.4, q=1.
Case 2. In the event that the equilibrium points lie on each side of H(X), the endemic equilibrium points E11 and E12 are real equilibrium points.
In Fig. 5, H(X) is located in the middle of the two equilibrium points, the trajectory tends to either E11 or E12, meaning that the trajectory tends to E11 at region S1, and the trajectory tends to E12 at region S2. This can indicate that the system is bi-stable.
Case 3. The equilibrium points are on each side of H(X) and the endemic equilibrium points E11 and E12 are virtual equilibria points.
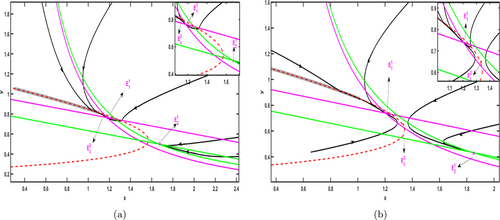
Fig. 5. Phase plane of the Filippov system of Case 2. The green and purple lines are the free system S1 and control system S2, respectively. The red line is the threshold line H(X), and the black line is the solution trajectory of system (3). The parameters of the subgraphs are denoted by (a) α=1.2, ET=0.52, a1=0.7; (b) α=1.3, ET=0.544, a1=0.75. The other parameters are, respectively, s=7, c=3, β=9, r=6, p=0.4, q=1.
In Fig. 6, H(X) is located in the middle of the two equilibrium points, all the trajectory lines are colliding with the threshold line and converge to the pseudo-equilibrium point E2c along the threshold line, so the pseudo-equilibrium point E2c is globally asymptotically stable.
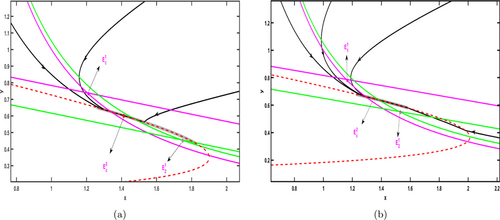
Fig. 6. Phase plane of the Filippov system of Case 3. The green and purple lines are the free system S1 and control system S2, respectively, the red line is the threshold line H(X), and the black line is the solution trajectory of system (3). The parameters of the subgraphs are denoted by (a) α=1.3, ET=0.44, a1=0.4; (b) α=1.1, ET=0.5, a1=0.38. The other parameters are, respectively, s=7, c=3, β=9, r=6, p=0.3, q=1.
Case 4. If H(X) lies on the lower side of the endemic equilibrium points of subsystem S1 and subsystem S2, the endemic equilibrium point E11 is a virtual equilibrium point and the equilibrium point E12 is a real equilibrium point.
In Fig. 7, trajectories from region S1 move along H(X) from right and from up to down, eventually converging to E12. Trajectories from region S2 converge directly to E12. Because the system has no limit circle, E12 is globally asymptotically stable.
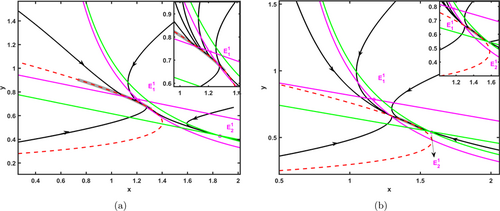
Fig. 7. Phase plane of the Filippov system of Case 4. The green and purple lines are the free system S1 and control system S2, respectively, the red line is the threshold line H(X), and the black line is the solution trajectory of system (3). The parameters of the subgraphs are denoted by (a) α=1.3, ET=0.53, a1=0.7; (b) α=1.1, ET=0.61, a1=0.65. The other parameters are, respectively, s=7, c=3, β=9, r=6, p=0.4, q=1.
6. Boundary Equilibrium Bifurcation
A boundary equilibrium bifurcation occurs when the endemic equilibrium collides with the boundary equilibrium point at a tangent point. In this section, we choose to change the value of ET and fix other parameters to determine and verify the occurrence of boundary equilibrium bifurcation.
The boundary equilibrium point of the system satisfies
After numerical simulations, it is concluded that the position of the tangent point changes as the position of the threshold line changes, while the position of the equilibrium points E11 and E12 doesn’t change. When the threshold line H(X)=0 passes exactly through the equilibrium point E11, a collision occurs, producing a boundary equilibrium bifurcation.
In Fig. 8(a), when ET=0.34, E12 is the true equilibrium point and E11 is the virtual equilibrium point, at this time there is one sliding segment. When ET decreases to 0.32, both E11 and E12 are virtual equilibrium points with two sliding segments, as shown in Fig. 8(b). When ET=0.3165, in Fig. 8(c), we can find that the threshold line H(X)=0 moves past the equilibrium point E11, and at this time, the equilibrium point E11 collides with the tangent point T12, and there is a boundary equilibrium bifurcation, which is recorded as E1B. At the same time, there are still two sliding segments. When ET changes slightly, ET=0.31, E11 is the real equilibrium point, E12 is the virtual equilibrium point, and sliding segments change in number, from two sliding segments to one sliding segment, as shown in Fig. 8(d).
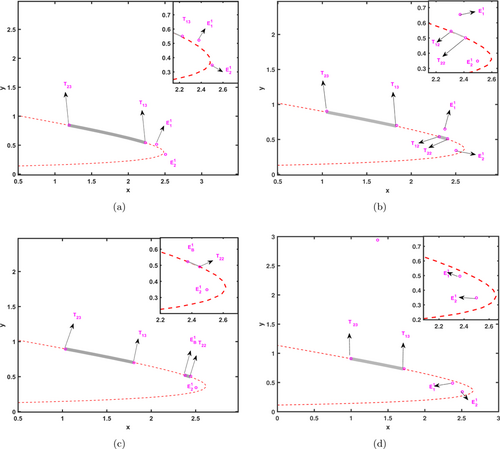
Fig. 8. Boundary equilibrium bifurcation illustration. The red line is the threshold line H(X)=0 and the gray line is the sliding segment. The parameters of the subgraphs are denoted by (a) ET=0.34, (b) ET=0.32, (c) ET=0.3165, (d) ET=0.31. The other parameters are, respectively, s=12, c=3, β=9, r=6, p=0.3, q=0.9.
7. Conclusion
The treatment of tumor is still a matter of concern. Many scholars have entered into in-depth research and thinking about tumor [Robertson-Tessi et al., 2012; Tang et al., 2015; Ren et al., 2017], however, the existing main considerations about tumor-immune models take the load of tumor cells or the load of immune cells as the switching state, and do not take into account the change rate of the tumor itself. This may also happen that the change rate of the tumor of the patient at a certain point in time is not controlled, causing irreparable damage to the immune system. Considering this situation, we simplified and improved the model based on [Li et al., 2021; Peng & Xiang, 2023], and added the change rate of the tumor into the switching condition to obtain a nonlinear threshold function H(X)=0. This consideration can intuitively monitor and control the change of the tumor, and analyze the behavior of the model from the point of view of the tumor control, which provides a realistic strategy for the timely detection and treatment of the tumor.
First, we discuss the dynamical behaviors of the two subsystems of the model separately and establish the sliding segments and its dynamical properties according to the theory of Filippov system, which assists us in analyzing the existence and stability of the pseudo-equilibrium points [Deng et al., 2021, 2022; Tang & Zhao, 2021]. Second, on analyzing the global dynamical behavior of the system, it is proved that the system has no limit circle, and according to the variation of the threshold function, we find that when the threshold function is higher or lower than the two equilibrium points, all the trajectories converge to one equilibrium point E11 or E12, as in Figs. 4 and 7. This suggests that the control system is difficult to trigger when the threshold function is too high, while the control system always triggers when the threshold function is too low. From a clinical point of view, this is meaningless for tumor control and treatment. Therefore, the selection of an acceptable threshold function is very essential. As threshold functions occur across the two equilibrium points, and both equilibrium points are virtual equilibrium points, the trajectory will eventually stabilize at the pseudo-equilibrium point. This indicates that the load of tumor cells can be maintained at the previous level, illustrated in Fig. 6. As the threshold function occurs between the two real equilibrium points, the trajectory will eventually stabilize to E11 and E12, as shown in Fig. 5, which is called the bistable phenomenon. In this case, the tumor cells will be kept under control and their number will be reduced to a low level.
Choosing an appropriate threshold function has a positive effect by protecting the tumor from further deterioration and treating the tumor. By adjusting the threshold function, we can control the growth and spread of tumor cells and keep them at a controlled level. This helps to curb the progression of tumor and reduce their damage to the organism. Therefore, the study and application of appropriate threshold functions are of great significance in the field of tumor prevention and treatment.
In fact, the current means and level of medical care are not able to completely cure the tumor, which include not only the number of eradicated tumors, but also consider the tumor and quality treatment measures to minimize the damage to the immune function of the patient. Thus, what we can do now is to reduce the load of tumor cells to a certain threshold level a little before the tumor reaches an uncontrollable point. This can be interpreted as controlling tumor growth and immune cell reduction with a desired trend. Based on the previous sections, we find that the equilibrium point at which the trajectory eventually converges is different when the correct parameter values are chosen in the case of the threshold function of H(X). From the clinical point of view, choosing a reasonable nonlinear threshold function to control the tumor cells can keep their load at a lower level, which provides a new idea for real-life tumor prevention and control.
Although we have found that nonlinear threshold functions produce rich dynamical behavior for tumor-immune model, the road to be traveled in tumor therapy is still long. In reality, the efficacy of drugs in the patient’s body has a certain delay, in the process of delay, we also need to consider the concentration of the drug, in addition, the different dosing cycles will have different effects on the tumor. These are all issues that require thinking and attention, and they are also the work we need to complete next.
Conflict of Interest
All authors declare no conflicts of interest in this paper.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No. 12361100).
ORCID
Hengjie Peng  https://orcid.org/0009-0006-8984-0373
https://orcid.org/0009-0006-8984-0373
Changcheng Xiang  https://orcid.org/0000-0002-9610-0289
https://orcid.org/0000-0002-9610-0289
| Remember to check out the Most Cited Articles! |
|---|
|
Check out our Bifurcation & Chaos |


