A Survey of Schematic of Vacuum Quantum Structure: General Equation for EBSF (III)
Abstract
Researchers have studied the tiny effects on fundamental particles with quantum vacuum about electroweak baryogenesis mechanism, and so we can further confirm the existence of the energy basic state field of the universe (EBSF). In this paper, we propose that since EBSF is the basic energy field of the universe, the quantum superfluid state must be the next level of fundamental particle (quantum state). Then, the evolution-developed equation of quantum superfluid state should be nonlinear, which can be expressed by the fraction fractal KdV equation temporarily. This paper reviews the experimental observation of superfluid in the existing physics and puts forward the possible quantized form of KdV equation. One possible form of quantization for vortex line of quantum superfluid is the string theory, so the basic physical scenario and foundation of physics in string theory can be revealed. At the same time, through the analysis of the KdV equation and general solution, the quantum superfluid state as the lowest level physical state in physics can only be described by the topological invariant in topological theory, and its image is not uniform; there are common phenomena such as energy gap, non-closure and wrinkle (folding) in Euclidean space. Based on the physical view of the formation of the universe system, the idea of nonlinear evolution development, and the idea of level emergence theory in condensed matter physics, the authors preliminarily put forward the framework of the hierarchy theory of physics. The paper also analyzes the broad physical prospect of quantum superfluid physics (or new physics). The essence of some physics concepts is further clear, some present physics puzzles that are expected to be solved, but their mathematical physical processing has considerable complexity, and some rigorous proofs need further breakthroughs.
1. Introduction
From the Dirac equation and the Klein–Gordon equation, the observed quantum superfluid phenomenon, and proton’s spin studies, it’s not difficult to arrive at a reasonable scenario where the next level of elementary particles should be nonlinear physically logically speaking. In general, there is only one kind of linear relation. The nonlinear relation is so varied that the equations describing nonlinear system are no longer simply following the superposition principle; in addition, each part of the nonlinear systems is no longer an independent proportional relationship, but they all influence each other, coupled together, resulting in the complexity and diversity of nonlinear problems, and eventually evolving a rich and colorful macroscopic physical world.
It has been found that nonlinear partial differential equations (NPDEs) have a class of meaningful and interesting isolated solutions from fluid-related phenomena. Isolated waves, whose shapes are not dependent on the interaction between them, have elastic collisions like particles, and the solitary waves with this property are usually called solitons. Since the vacuum of the universe is indeed the fundamental energy field of a special quantum superfluid, then a comprehensive and systematic study of the evolution of the universe, a comprehensive and system study of the formation of celestial bodies, matter and particles will be possible; it would also be wonderful to combine the soliton theory and integrable systems with applied mathematical physics in a perfect way. The world is nonlinear by nature, and linearity is only a special case of nonlinearity or an approximation under certain physical conditions. We also need emergent phenomena theory (EPT or Hierarchical Display Theory), which will tell us how to evolve from the basic energy field of quantum superfluid (dark energy field) to elementary particles, to atoms and molecules, and finally to celestial bodies, as well as their interactions, or the internal physical logic and laws of physics between layers (levels).
However, nonlinear and systems-oriented physics are very complex indeed, and we are still thinking deeply about finding out from our college days to the present age of “knowing the fate decreed by Heaven”. But we firmly believe that we are not alone.
It is generally believed that quantum electrodynamics (QED) and quantum chromodynamics (QCD) are in fact low-energy effective field theories, which fail at high energy conditions like Planck energy, fail at ultra-low energy conditions, and must be replaced by more complete theories. This is matter of course, in short gravity it is already strong and can no longer be ignored at ultra-high energies, and a complete theory of physics must include gravity; it would also have to take into account quantum effects of space-time and dark energy fields. In physics, in the past, the Planck scale was a natural truncation of QED and QCD divergence. We won’t have a complete theory right away, but it will provide a clue to the more fundamental physics of QCD. In addition, we cannot presuppose that in the ultra-low energy quantum physical state, the space-time is three-dimensional of Euclidean space plus time’s dimension, or is fully satisfying four dimensions of general relativity, which requires physical verification. It should have an evolving law; there may be a physical phenomenon of “dimensional transmutation”, so in fact some of our research in ultra-low energy quantum superfluid may only be an image in Euclidean space plus time’s dimensional, which comes from real time-space. That’s not the focus of this paper, so this paper focuses on Euclidean space-time, unless otherwise noted. We don’t think there is a “theory of everything” that applies to all physical phenomena.
In,2 we conclude that a new view on the dark energy of the universe can be formed accordingly, all physical objects in the universe, together with empty space, rest in a “sea” of such kind of EBSF and maybe display negative energy (not macroscopic statistical “zero- point energy”). In this energy region, the energy is in the negative pressure region with no static-state mass. There is no strong interaction and electromagnetic mechanism with other physical particles and there are no observable particles. It is an energy region dominated completely by wave function, which takes on energy level characteristics and conforms to Pauli exclusion principle. It can be simply imagined as a quantum superfluid with physical properties such as no static-state mass, no viscosity, ubiquity and negative pressure.
Also, it is the core content of EBS evolution to derive the solitary wave and the soliton. In that paper, it is present that EBS’ evolution development can be described in terms of the historically famous like-KdV equation, which is commonly known as the Korteweg–de Vries :
Nonlinear partial differential equations (NLPDEs) have a lot of applications in different branches of mathematics, physics, and engineering. NLPDE describes the various phenomena in nonlinear optics, engineering, plasma physics, chemistry, mathematical biology, etc.3,4,5,6,7,8,9,10,11,12,13,14 Extracting exact solutions for these equations is often a complicated task, so finding powerful and effective methods is still a point of attraction to a diverse group of researchers. The G′/G-expansion method,15 inverse scattering method,16 tanh function method,17 Lie symmetry analysis,18,19,20 Jacobi elliptic function expansion method,21 the Bäcklund transformation method,22 Darboux transformation method,8,9,23 Hirota’s bilinear method,24 solitary wave ansatz method, F-expansion method, multiple exp-function method, Kudryashov method,25 and many others are some powerful and systematic approaches. Among these techniques, GERF method26,27,28,29,30,31 seems an efficient approach that holds significant features that make it practical for the determination of solutions to various NLPDEs.
At the same time, the basic KdV equation has been modified to multi-type nonlinear KdV equation such as KdV–Zakharov–Kuznetov (MKdV-ZK),32,33 modified–mixed KdV equation,34 KdV–mKdV equation,35 nonlinear variable-order fractional Korteweg–de Vries equations,36 damped Korteweg–de Vries (KdV) equations,37 generalized Hirota–Satsuma coupled KdV and MKdV equations,38 Schamel–KdV equation with constant coefficients,39 variable-coefficient compound KdV-Burgers equation.40 coupled KdV equations,41 Extended KdV equations generated by squared eigen-function symmetry,42 KdV–Caudrey–Dodd–Gibbon equation43 and so on.
This paper focuses on the analysis of the solution of KdV equation on general equation for EBSF and its related physical significance. In Sec. 2, the size scale of the next layer of elementary particle is proposed. In Sec. 3, we describe in detail the research content of Michael Dine on sphaleron baryogenesis at the electroweak phase transition in the Standard Model, which established confidence for us to propose ESBF and the study of the whole paper, although we think their estimate of the ultra-weak effect in the non-Abelian case is incorrect. In Sec. 4, we show our latest research progress of KdV equation in mathematical physis, and point out the general development equation of EBSF energy basic state field—KdV equation. In Sec. 5, we discuss how to localize and quantize for the evolution and development equations of EBSF. In Sec. 6, we discuss some physical questions. For example, the evolved development of EBSF is not uniform and there also exist energy nonlinear distribution and energy gap, having wrinkles, which are not closed under general physical conditions, in the extremely microscopic region. In Sec. 7, we put forward the preliminary framework of the hierarchy Hierarchical Display Theory of physics, and also analyze the broad physical prospect of quantum superfluid physics (New Physics).
2. The Physical Size Scale of the Study
Since the object of study is the object of the next levels of elementary particles, the scale is below 10−19m, and the greater limit is known as the Planck scale.
We still need to explore some of the physics of the nearly Planck scale. The Planck length is extremely tiny, about 20 orders of magnitude smaller than the nucleus of an atom. On a logarithmic scale, however, humans are much closer to the Planck length, associated with the Planck length are the Planck time, the Planck energy and the Planck mass. Generally speaking,
Although the Planck length is much smaller than atomic nucleus, the Planck energy is much higher than the 103GeV or 1TeV that the present particle accelerators can achieve, in our normal study area, this limit is far from being reached, and this paper studies the ultra-low energy region. As the interaction energy approaches the Planck energy, the strength of gravity becomes roughly equivalent to the strength of the other fundamental forces. The gravitational force between two particles of mass m is Gm2/r2, and the electrostatic force between two electrons is e2/r2. If there is m2≈e2/G, the forces are equal, but if e2=ℏc/137, they are orders of magnitude closer, and this mass is the Planck mass.
As we all know, the quantum superfluid state of the Planck scale can be described by physical quantities such as the order parameters of the macroscopic (elementary particle level length 10−20 m). It has superfluidlity, so it cannot be assumed that it can be described by the four-dimensional relativistic space-time, or Euclidean space plus time’s dimension, but its real dimension should also be Φ(ε,x,ϕ,τ), In other words, in addition to the time and space dimensions, the description of EBSF’s excited states also requires the characterization of quantum order parameters and vortex linear density of quantum superfluid, which is rather complicated.
3. Yang–Mills Vacuum Structure and Related Physical Treatment
People have researched tiny effects on fundamental particles with quantum vacuum about electroweak baryogenesis mechanism. Although the following research content is mainly concerning sphaleron processes and violation baryon number, the analysis of the effect of vacuum energy on elementary particles using the mathematical physics method is also a topological invariant of the electronic band of the last century—Chern–Simons number— but the physical idea is very rich, the understanding of vacuum quantum energy field has also made progress, we do not hesitate to the elaborate,44 as follows:
In the literature,44 in order to study sphaleron processes, Yang–Mills theory is refined and it is believed that the vacuum energy field can be expressed as Fig. 1.
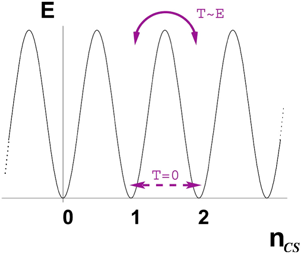
Fig. 1. Schematic Yang–Mills vacuum structure. At zero temperature, the instanton transitions between vacuum with different Chern–Simons numbers are suppressed. At finite temperature, these transitions can proceed via sphalerons.44
Earlier, people stated that the renormalizable interactions of the Standard Model preserve baryon and lepton numbers. This statement is valid classically, but it is not quite true of the quantum theory. Very tiny effects with quantum vacuum (’t Hooft, 1976) exist. These effects are tiny because they are due to quantum-mechanical tunneling, and are suppressed by a barrier penetration factor. First, it is conceivable that these sphaleron processes can themselves be responsible for generating a net baryon. This is called electroweak baryogenesis (Kuzmin, Rubakov, and Shaposhnikov, 1985). Second, as we will see, sphaleron processes can process an existing lepton number, producing a net lepton and baryon number. This is the process called leptogenesis (Fukugita and Yanagida, 1986).2,44
One of the great successes of the Standard Model is that it explains the observed conservation laws. In particular, there are no operators of dimension four or less consistent with the gauge symmetries which violate baryon number or the separate lepton numbers. The leading operators which can violate baryon number are of dimension six, and thus suppressed by O(1/M2). The leading operators which violate the separate lepton numbers are of dimension 5, and thus suppressed by one power of 1/M. In each case, M should be thought of as the energy scale associated with some very-high-energy physics which violates baryon or lepton number. This scale cannot be determined except through measurement or by specifying a more microscopic theory.
However, it is not quite true that the Standard Model preserves all of these symmetries. There are tiny effects which violate them of order
One might think such a violation of current conservation would lead to dramatic violations of the symmetry. But the problem is subtle. The right-hand side of the anomaly equation is itself a total divergence :
In non-Abelian theories, however, there are no perturbative field configurations which contribute to the right-hand side. These lead to violations of baryon number and the separate lepton numbers proportional to e−2π/α, where α is the coupling constant of the theory. These configurations are called instantons. A pedagogical treatment is given by Coleman (1989). They correspond to the contribution of a tunneling amplitude. To understand what the tunneling process is, one must consider more carefully the ground state of the field theory. Classically, the ground states are field configurations for which the energy vanishes. The trivial solution of this condition is →A=0, where →A=0 is the vector potential. More generally, one can consider →A=0 which is a “pure gauge,”
So the ground states of the gauge theory are labeled by an integer n. Now if we evaluate the integral of the current K0, we obtain a quantity known as the Chern–Simons number:
In Fig. 1, at weak coupling, we have an infinite set of states labeled by integers and separated by barriers from one another. In tunneling processes which change the Chern–Simons number, the baryon and lepton numbers will change because of the anomaly. The exponential suppression found in the instanton calculation is typical of tunneling processes, and in fact the instanton calculation which leads to the result for the amplitude is nothing but a field-theoretic WKB calculation.
At zero temperature, the decay amplitude is suppressed, not only by e−2π/α, but by factors of Yukawa couplings. The probability that a single proton has decayed through this process in the history of the universe is infinitesimal. But this picture suggests that, at finite temperatures, the rate should be larger. One can determine the height of the barrier separating configurations of different nCS by looking for the field configuration which corresponds to the barrier saddle point. This is the sphaleron solution of the static equations of motion with finite energy (Manton, 1983). When one studies the small fluctuations about this solution, one finds that there is a single negative mode, corresponding to the possibility of rolling downhill into one or the other well. The sphaleron energy Esp has the form
What the authors need to further elaborate is that the above research points out there is a “ground state of the field theory” and puts forward a “pure gauge”, which requires a matrix of gauge conversion when the quantum field of particle is converted, and puts forward “h”- a gauge transformation, which is called “small gauge transformation”. Of course, in Abelian transformations, →A=0, fixing the gauge eliminates all but the trivial solution. This is not the case with non-Abelian transformations, which require Chern–Simons number numbers to mark.
The above research shows that, indeed, to further explore physics, it is necessary to establish a correctly described vacuum quantum field structure, even though this quantum field structure is rarefied and is an extremely weak field, in order to correctly deal with these microscopic actions and action transitions. The above research can also generalize or confirm the existence of the energy basic state field of the universe (EBSF).
The calculation of formula (4) is in the framework of the original fundamental particle standard model. The authors argue that this calculation is significantly undersized, as can be seen in the relevant analysis of vacuum energy in.1
Obviously if EBSF exists, it must be everywhere, including those less than 10−20m that cannot be detected by human experiments up to now. It’s possible EBSF quantum states in other gauge fields may be different from those of vacuum EBSF quantum states, this is indeed also a nonlinear development problem. That is to say, the EBSF quantum states that exist in particles are more complex when there is gauge transformation of the main quantum field.
These also remind us of the discovery fractional quantum Hall state by Cui Qi. Later, some theorists in condensed matter physics developed a physical theory based on a spin liquid, in which electrons charged at same time with spin appear to spontaneously split into spin only and charged hole only under certain physical conditions. The holes are bosons, whose Bose condensation can lead to high-temperature superconductivity. There are many types of spin liquids that can produce high-temperature superconductivity, including chiral liquids (which break parity symmetry), which were proposed around 198845,46 and 1991 Z2 spin liquid (described by Z2 gauge field).47,48 Although in theory they are self-consistent and have been implemented in some numerical models, these spin liquids have not been found in experimental materials for about 30 years. In my opinion, it is not ruled out that these spin liquids can also be explained by EBSF special states or by interactions with main quantum states.
4. General Equation for EBSF Evolution Development
4.1. Possibility of EBSF development expression by KdV equation
In recent decades, a large number of nonlinear phenomena have been discovered in many research fields such as physics and fluid dynamics, which can be described by mathematical models of nonlinear evolution equations. The nonlinear evolution equations (NLEEs) have been continuously traced to many innovative applications and remarkable progress has been made in the contribution of the exact solutions for nonlinear partial differential equations, which have been a basic concern for both mathematicians and physicists. The diversity of their solutions reflects the various forms of space-time structure of the matter world. But because of the complexity of mathematics, it is extremely difficult to find the exact solution of the nonlinear evolution equation. If the traveling wave solution is found, the nonlinear partial differential equation can be changed into nonlinear ordinary differential equation. In particular, the generalized KdV equation can be used to establish effective mathematical models for the physical phenomena of Bose–Einstein condensate BEC and Plasma phonon, so that the Bose–Einstein condensate of weakly interacting atomic gas can be simulated by studying the nonlinear properties of physical waves. The nonlinear excitation theory research and phenomenon support the new field of nonlinear atomic optics; the use of KdV equation to describe the EBSF provides the possibility.
As can be seen from Fig. 1, it is itself a conditional solution of the KdV equation in.39 Intuitively speaking, the quantum vacuum mode shown in Fig. 1 should only be a mode under certain physical conditions.
As described in,2 EBSF should be a special KdV-like equation, and it interacts with other physical fields to evolve and transform more extensively. The physical symmetry of EBSF is very good and it should have a lot of physical symmetry. Secondly, it should be related to the Schrödinger equation. More importantly, it can be used to describe quantum superfluid development state. See Ref. 1 for more physical ideas.
4.2. KdV equation
Based on the famous Boussinesq equations in shallow water wave theory, the classic KdV equation is derived by using reduced perturbation method above, we still use the potential ε to characterize.
We know that the standard KdV equation is as follows :
Let u(x,t)=S(ξ),ξ=x−Kt, to solve the above formula
The KdV equation has isolated wave solutions with arbitrary constants to be determined and waveform invariance.
When C=−ξ0, the graph of formula (18) is shown in Fig. 2.
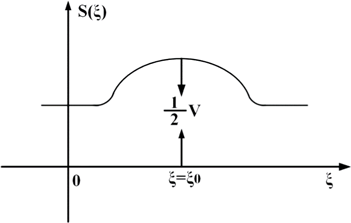
Fig. 2. The graph of an isolate wave solution.
The isolated solution of the KdV equation is obtained by the usual integral method, but it is not sufficient for the purpose of discussing the collision of isolated waves. For another solution of the KdV equation, the KdV equation is reduced to an easily solvable form by means of the technique of Cole–Hopf transformation, namely the transformation equation method.
Let :
We obtain
In order to find a new solution, the usual method of finding a particular solution of a nonlinear equation is given :
The characteristic of this equation is that its non-homogeneous term depends on the solution of the preceding equation therefore, so if the solution F(1) of the first equation is found, then the solution F(2) of the second equation, as a linear non-homogeneous equation, can also be found. Thus the third equation…, is the k linear equations, both of which can be solved.
Now let the solution of (23) be
Its solution can be easily obtained as
If ς=1 (otherwise, ς=e(logς) can be absorbed into the exponent), the exact solution is
In general, if the solution is chosen as follows :
So, when N=1,2,3,…,n, find a series of exact solution to the equation.
So we get a series of isolated wave solutions,
Nonlinear distortion is inevitable in the process of nonlinear wave evolution. In the above, an analytical process of the general nonlinear KdV equation is described in detail, trying to understand whether there is quantization, condensation localization and other physical phenomena during the evolution and development of the nonlinear KdV equation. However, up to now, we have not reached a definite conclusion. In this extremely micro region, the hints given by nature are very rare.
From a mathematical physical point of view, the evolution of the universe, the change of nature, is itself a mathematical transformation. In the physical world where we study such tiny scales and such short timescales (under picoseconds), these mathematical physical transformations richly exist anyway, they are complex and non-continuous, but it is difficult for humans to find them and apply them.
4.3. General equation for EBSF, fractal fractional KdV equation
Nowadays, various techniques are used to find the solutions to nonlinear partial differential equation, NLPDEs are challenging for researchers to solve, they employ a variety of methods to do so. The following briefly introduce some related researches in conjunction with quantum superfluid.
(1) Fractional equation
In the literature,41 Shao-Wen Yao et al. used the fractional beta derivative and considered the fractional beta derivative operator. The given fractional NLPDEs are transformed into nonlinear ODEs by using suitable transformation with fractional parameter. And then determined the new solitary waveform solution for the coupled KdV equation and the coupled system of variant Boussinesq equations with beta time derivative.
Let μ(τ) be a function defined for all non-negative τ, fractional derivative of μ(τ) of order β is given by49
Theorem:
Let μ(τ) be β-differentiable function for all t > 0 and β⊂(0,β],
Let the equations be
Let the system of nonlinear PDEs be converted into system of nonlinear ODEs by supposing the transformation.
Then, the system (37) becomes
The solutions of the coupled KdV equations are shown in Figs. 3 and 4.
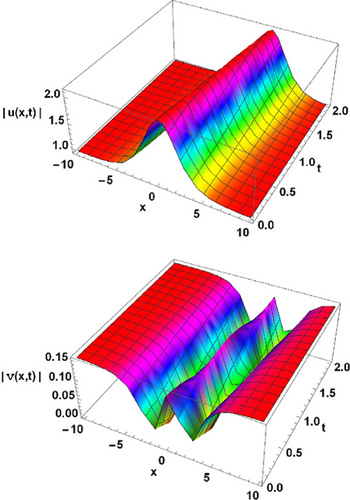
Fig. 3. 3D and 2D graph when ω1=−0.5, κ1=0.4, γ=−0.5 and λ=−0.3.49
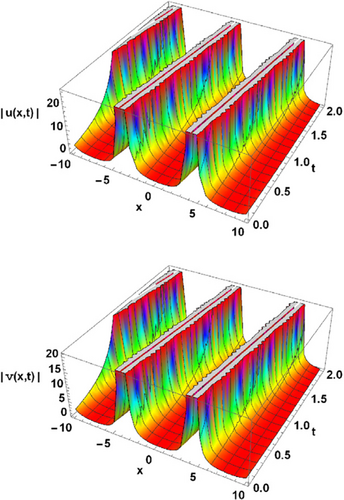
Fig. 4. 3D and 2D graph when ω1=−0.5, κ1=0.4, γ=−0.5 and λ=1.41
See Ref. 41 for detailed calculations and graphs.
(2) Using nonlocal Caputo fractal-fractional operator
Abdul Jamal et al.35 proposed a new kind of KdV equation, so-called KdV–mKdV equation by combining KdV and mKdV as follows :
Abdul Jamal et al. observed that“Several real-world problems have been analyzed by using fractional calculus (FC) with better memory effect. The traditional calculus which is failed to study some memory features of different problems that occur engineering and science, was generalized to become FC.” The authors deal with the definition of Caputo fractal-fractional operator and J-transform. The authors obtained some particularly meaningful results, see Figs. 5 and 6, see Ref. 35 for a detailed process.
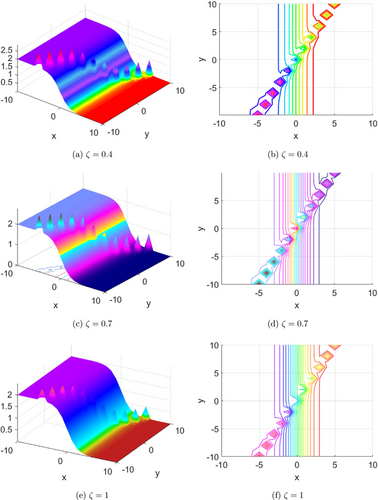
Fig. 5. Evolution of the solution of problem 1 for ζ=0.4, 0.7, 1 and ϖ=1.35
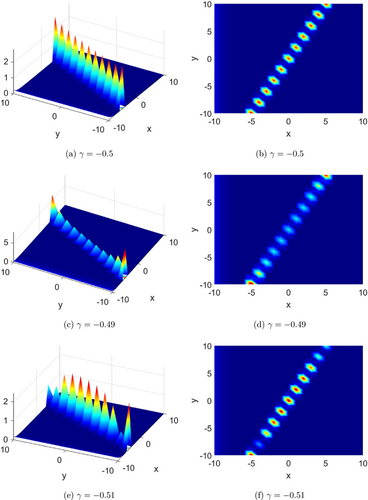
Fig. 6. Effects of the parameter γ on evolution of the solution of Example 1.35
In the literature,35 the authors showed that the solution of considered problem under the considered operator exists and is unique, and concluded that the solution of the problem has been deduced by using J-transform with Adomian decomposition technique, the convergence and stability of the suggested method have been verified via nonlinear analysis and Picard-stability.
In the literature,50,51 Sirendaoreji et al. studied equation of mKdV, Boussinesq, sine-Gordon and the nonlinear Klein–Gordon, respectively. Zhang et al.52 computed the exact solution of the nonlinear mKdV equation given as
5. Quantization of the Evolution and Development Equations of EBSF
An important physics problem is how to quantize EBSF evolution equation? To answer this question, we must return to the scientific observations that have been made about superfluid.
The following experiment observations on superfluid are from the Ref. 54
This annular quantize of superfluid mechanics can be seen taking 4He as an example, it is quantized in units K=ℏm=9.98×10−8m2⋅s−1. The most compelling evidence was proposed by Richard Feynman. The existence of quantization of ring quantities has been shown experimentally, the quantum value of which was confirmed by Vinen in 1961. The quantum condition explains the stability of continuous flow: no continuous process can change the value of n, which is a topologically stable quantum number. So, what happens if you apply the above formula to a simply connected region of liquid? There is no void to prevent our integrating loop from continuously contracting to zero, so something strange must happen, if n≠0. Suppose n=1, integrate along a small circle of radius, r, Vs=ℏ/(mr), where r is the atomic scale, vs is the magnitude of the speed of sound, and the macroscopic concept fails. There must be a node in the wave function, there must be an atomic scale region in which the superfluid is suppressed. If you think about it, the nodes must take the form of lines in a liquid, and what we get are vortex lines, like those you see when you empty a bathtub, only much weaker. Forming such vortices and moving from one side of the flow channel to the other is one possible mechanism for sustained flow decay. Vortices with n>1 may not be important because their energy is proportional to n2, thus preferring the presence of n single quantum vortices.
From the above observations, the symmetry breakdown of quantum superfluid first forms a node (soliton) of the quantum superfluid, then forms vortex lines, and then forms the entanglement of vortex lines.
To understand the continuous flow of the quantum superfluid from the macroscopic wave function, the length of the annular channel must be an integral multiple of the de Broglie wavelength, or to put it another way, the change in phase must be a corresponding phase change of position change dl.
In this way, it is given by integrating around the annular channel
It can be more convenient to take dl as the displacement component parallel to Vs, and the above equation can be rewritten as
Evidence for vortex lines and arrays of quantum superfluid was first obtained by Vinen and Henry Hall in 1956 from the second acoustic experiment. They found that in uniformly rotating helium II there was an additional attenuation of the second tone, the magnitude of which was proportional to the angular velocity. This can be explained by the following mechanism: Because the thermal excitation is scattered by the vortex lines, there is a drag that prevents the reverse convection of the normal flow and the superfluid current. The fact that the density of vortex lines is proportional to the angular velocity cleanly explains the observed results. More direct evidence was obtained by Packard and his colleagues, who took advantage of the fact that negative ions (a bubble containing an electron) were attracted to the vortex core (forming a chain of bubbles), attached electrons to the vortex core, applied an electric field to pull the electrons away from the surface of the liquid, magnetically focused them onto a fluorescent screen, and took a photograph showing where the electrons had escaped on the surface of the liquid the image. The first evidence of discrete vortex lines was obtained in 1974, after which efforts were made to reduce the vibration of the electron escape point and it was not until 1979 that an array of points stable in rotating coordinate system was made obtained. Each vortex line moves in the velocity field generated by all the other vortex lines, thus rotating with the container.
Implications for the quantum superfluid of liquid 4He: The phase transition of liquid 4He at 2.17K was first noticed through a small anomaly in the density of the liquid, and then was found to be accompanied by sharp anomalous heat capacity peak shaped like a Greek letter. Therefore, the phase transition place is called the entry point and the transition temperature is denoted as Tλ. The high temperature phase corresponds to helium I, and the low temperature phase to helium II.
The experiment proves that the two-fluid model describing Helium-II, the total density of the liquid ρ, is divided into two parts: The normal part ρn, which behaves like an ordinary liquid, and the superfluid parts ρs, which has no flow resistance. The ratio of the two parts transitions smoothly from being all normal liquid at a Tλ temperature to all superfluids at absolute zero. In 1914, Landau’s idea of thermal excitation in the ground state of quantum mechanics of liquids provided the theoretical basis for this model. According to this theory, the total entropy of a liquid is related to that of a normal fluid, so a superfluid thermal effect is expected. In the superfluid part, the fluid rushes so sharply toward the heat source that a fountain is formed. The thermal effect is shown more quantitatively in the second acoustic phenomenon, which travels as temperature waves. In the usual system, temperature changes rapidly; up to 1m below the surface, there is little change in temperature from one year to the next. But in helium II, the temperature can travel as a wave, and the normal and superfluid move in opposite directions, so the compression of the normal fluid corresponds to the thinning to the superfluid ( Thus, we obtain the physical mechanism of the nature of the formation and annihilation of particle and negative particle, which we still discuss in detail in a future article). The second sound wave travels depending on the temperature at about 20ms−1, an order of magnitude slower than the normal speed of sound. In ordinary sound waves, the two fluids move together, creating a pressure wave that travels at about 240ms−1.
Experimental confirmation of the two-fluid model suggests that the apparent similarity between ordinary quantum superfluid and the Bose condensate of an ideal Boson gas should be taken seriously. In temperatures below T0 magnitude, a portion of the atoms in the gas will be in the lowest energy state. This ratio increases with decreasing temperature until it reaches 1 at absolute zero. The phenomenon has been demonstrated and studied extensively over the past few years. People have tried to equate the ratio of superfluid components in helium II with the share of Bose-condensed atoms, because they share a common wave function; But this is wrong. The fraction of zero-momentum atoms in helium II can be estimated by neutron scattering experiments. If the energy of the neutrons is high enough, the scattering process is essentially monatomic scattering, and the momentum distribution of the scattered atoms can be calculated using the “pinball” model. Comparisons with experiments show that only 10% of the atoms are in a zero-momentum state at absolute zero, even though the liquid is 100% superfluid.
We conclude that the ground state wave function of liquid helium is more complex than a simple Bose condensate due to the strong action in the liquid, but the properties of the superfluid do indicate that the concept of macroscopic wave function can be applied to the entire superfluid component. This means that whatever be the ground state wave function, it must be strongly correlated, possibly involving associated pairs of zero-mean-momentum atoms, and perhaps combinations of four atoms. Thus, the order parameter, in the form of a macroscopic wave function, is sturdy with respect to the introduction of the interaction, while the portion of the condensate is not. In fact, an ideal Bose gas is a limiting case where it is infinitely compressed below the condensation temperature, and the effect of squeezing is simply to push more atoms into the ground state.
Solid helium-4 has a more severe deviation from the ideal gas, but a recent work by Kim and Chan suggests that even this system shows super-prevalence, although the superfluid component is only about 1% at T=0, and the proportion of Bose condensation may be lower. The possibility that this effect exists was first suggested by Leggettd in 1970. The essential different between a fluid (liquid and gas) and a solid is that the probability of finding an atom in a fluid is spatially uniform, whereas in a solid the probability of finding an atom is high near the lattice points and low between them. It has been argued that the very low probability between lattices limits the amplitude of any macroscopic wave function, and therefore the maximum share of superfluid properties is indeed extremely difficult to completely disappear.
From the above experimental observations, a reasonable analogy can be made. The quantum superfluid in EBSF first forms a series of nodes, which gives rise to the topological relationship and finally into the vortex lines (order parameters) of the quantum superfluid, and even generates under certain physical conditions. It seems that this topology relationship exists forever regardless of how quantum superfluid evolve, and this is also verified by quantum entanglement.
It seems that the origin of space-time also stems from this topology. Then, from the KdV equation of quantum superfluid evolution, the resulting Euclidean-space and time must be uneven.
By analyzing Formula (34) and Figs. 3–6, it is not difficult to get the general characteristics of the picture described by the KdV equation: it is full of wrinkles and gaps, there also exist energy gaps which are unclosed in a larger scale range. This should be the microscopic origin of the uneven space-time of general relativity.
The above observation of physics experiments is mainly for the observation of superfluid of relatively macroscopic molecular series generated under certain physical conditions or rotations. So what are the possible ways or consequences of quantization of the thin, ultra-weak quantum superfluid state in a vacuum?
How does quantum superfluid state cluster, localize and quantize? These microscopic rules can be further studied by the KdV equation.
David Wallace has a profound understanding of the nature of matter, and in his paper,54 his views pertain to future. He concludes that matter comes in particle and antiparticle forms, and does so in some cases and not in others, because of the following aspects:
| (a) | Particles are emergent phenomena, which emerge in domains where the underlying quantum field can be treated as approximately linear. | ||||
| (b) | The wave functions of those particles obey the complexification of the linear dynamical equations governing the (linearization of the) underlying field. | ||||
| (c) | As such, the internal symmetry group of a particle is the complexification of the internal symmetry group of the underlying field. | ||||
| (d) | As a matter of group theory, if an irreducible real representation of a group is complexified, it will either remain irreducible, or fall apart into two irreducible conjugate representations. In the first case, there will only be one species of particle; in the second case, there will be two species, and the CPT theorem ensures that the two species do not differ intrinsically (in terms of mass, charge, spin, etc.) but only relationally. | ||||
| (e) | Both cases occur in nature. | ||||
In the existing literature, superfluid vortex arrays and other clustering phenomena in superfluid have been observed in detail. See53 for details. It was an eye-opener, these physical phenomena are unique and colorful.
Based on the above observations, we reasonably believe that the general quantization and localization process of quantum superfluid are as shown in Figs. 7–9.

Fig. 7. Quantum superfluid node or order parameter coherence.

Fig. 8. Clustering of quantum superfluid (localization).

Fig. 9. Quantum superfluid clusters have “domain” and “normal”, and the coherence length (∼10−25m) can further form quasi-particles, in which “domain” is the prototype of space-time, and “norm” is the prototype of field.
Usually from theoretical point of view, order parameters express a coherence of the quantum phase over macroscopic distances. In this sense, the superconductivity of metals is a form of superfluid. Ginsburg and Landau, in their 1950 phenomenological theory, describe this coherence in terms of an order parameter represented by a complex scalar field :
We try to deal with the relation law of evolution of these physical levels through higher-order category discipline. The evolution of Figs. 7–9 is also called topological excitation,1 which can get some enlightenment from the study of quantum topological physical states in recent years.
String theory also seems to offer a solution. Some hypotheses and foundations of string theory have not been introduced in this paper. Here, it has to be said that although it is full of mystery and puzzle, at slightly larger microphysical scales, the formation of quantum strings, super-branes, etc. by the emergence of excitation clusters of quantum superfluid states also seems to be a possible physical scenario under certainly physical condition, if it is true, which can be inferred from the nonlinear evolution of KdV. But we think that even though string theory is a special form of quantization and localization of quantum superfluid, it is not the whole of physics. There are other possible ways.
6. Quantum Superfluid States and Quantum State
6.1. Quantum state and quantum superfluid states
We try to establish some clear physical concepts. Quantum states of elementary particles satisfy the principle of linear superposition, while quantum superfluid states are nonlinear and integrable under general physical conditions. Mathematical and physical processing of linear quantum states has run through the development of quantum mechanics for nearly 100 years, and the description of quantum superfluid states is also analyzed in Ref. 1, here there will be no further discussion. How quantum superfluid states evolved into quantum states is our focus and should be the subject of our future research. The quantum superfluid states evolved from EBSF are described by KdV equation, however, from the introduction of Sec. 4 and so on, although the application of KdV equation solves some scientific problems in physics and other disciplines, it is somewhat disappointing: the current research results cannot establish a rigorous and scientific physics of quantum superfluid physics. If the quantum superfluid physics is established correctly, the cosmological constants of general relativity can be deduced through mathematical physics. But it still provides us with scientific clues, maybe the possible mathematical treatment will be more complex. We firmly believe that the physical idea is correct.
6.2. Consideration of fractional fractal KdV equation as evolution equation of quantum superfluid state
The KdV-like equation was chosen to describe the quantum superfluid mainly because it describes the nonlinear evolution development equation, in addition, to the following reasons.
(1) Conservation law
The KdV equation has an infinite number of conservation laws, which is an important reason why it can describe quantum superfluid. Simply, conservation of momentum and conservation of energy can be simply deduced. Our expectation is that the wholeness of the particle τ, during its lifetime, can be represented by these especial physical operators, maybe it’s a series physical operator. That is, for the duration of τ, these operators are invariant with respect to τ and x.
We can understand that linear superposition of quantum states only is a physical property of quantum state.
(2) The relationship between KdV equation and Schrödinger equation
Due to the principle of minimum energy, when the quantum order parameter in EBSF is present, the physical quantity is generated with a potential ε. The original complete symmetry is lost, and the physical quantity is generated. It can be simply understood as the possible potential that returns to the original complete symmetry state, which is called the Yang potential, and it is a probabilistic potential. Wave function is complex and there is not much significance to study it, thus, it is reasonable to use Yang potential instead of wave function to characterize the physical characterization of quantum superfluid. The potential is a relatively macroscopic quantity, just like other order parameters. According to the observation of existing quantum superfluid, some quantum superfluid has viscosity. Losing the properties of an ideal quantum superfluid, the standard form of potential ε is ε0+iε1, however, for the sake of simplicity, we still only discuss the real numbers for the rest of this paper.
Thus, replace u in Eq. (1) with ε
If ε(x,t) is taken as potential in Schrödinger equation of physics, the potential in ψxx−[ε(x,t)−λ]ψ=0, ε(x,t) is the solution of the formula (46). As mentioned above, this potential is the possession potential of the vacuum field, also known as EBSF, which is different from the potential energy of fields such as electromagnetic field, strong interaction field, and Higgs field. In the future we will study the evolution development in various fields in depth.
It can be seen that the KdV equation has many natural connections with quantum mechanics.
| (a) | It is shown that for every discrete eigenvalue of Schrödinger equation, there will be a KdV equation soliton corresponding to it, and vice versa. | ||||
| (b) | Further research shows the solution method IST of KdV equation can be regarded as the work of Riemann–Hilbert linkage value problem. | ||||
| (c) | In the study of nonlinear development equation, the concept of prolonggation structures was put forward, and the conservation law was unified in a new pseudopotential, which has similar unique characteristics with Yang potential ε. | ||||
| (d) | The results show that the nonlinear development equation, the nonlinear Schrödinger, Boussinesq equation and the Toda lattice vibration equation, can be taken as a completely integrable Hamilton equation of motion. | ||||
It should be noted that the general representation of EBSF, in my opinion, only describes the situation of node and vortex lines generated by EBSF, more cannot describe quantum turbulence, which is similar to the general fluid mechanics.
(3) Another core assumption of quantum mechanics
However, in quantum mechanics, there is the basic core of assumption that a quantum state φ (can be normalized) is a “vector” in Hilbert space, the common eigenstate Ψk of any complete set F in system, which represents commutative mechanical quantities (k represents a complete set of quantum numbers and is assumed to be a discrete spectrum), and can be used to form a set of orthogonal normalized complete base vectors of this state function space (called F representation), (φk,φj)=δkj, φ=∑kαkφk, αk=(φk,φ).
We have a set of Hermitian operators that are independent of each other and commutative ˆA(ˆA1,ˆA2,…), their state is denoted as φα, wherein α represents a set of complete quantum numbers. If α set of quantum numbers is given, the only possible state of the system can be determined, then it is called (ˆA1,ˆA2,…) which constitutes the systemic complete set of commutative observable measurement set of mechanical quantities and also corresponds to the complete systemic set of mechanical quantities.
From the above, it can be seen that quantum mechanics deals with special “quantum states”, and these quantum states are only at the “particle level” (scale 10−15m, E∼KeV–MeV). However, the description of physical reality in terms of wave functions is incomplete, although quantum mechanics’ description of the particle level is self-consistent.
A quantum state is only a particle-wave-level understanding of the way matter exists and works. The understanding below the level of elementary particles must be developed and understood from the perspective of quantum superfluid physics.
7. Some Possible Physics Perspectives
Although our study of EBSF has not established a rigorous discipline, we believe that the physical idea of EBSF is correct. The physical world around the absolute temperature is a rich physical world, humans have not known the physical world, its evolution and development — new physical is more complex than the mature physics, is a nonlinear world, there are complex, colorful nonlinear evolution processes. However, we can study physics from a broader physical perspective and a broader physical field of vision, understand and master the physical world from a richer mathematical physics method, and then enrich and develop this physical scenario with a rigorous mathematical physics method, at the same time, the essence of some physics concepts are clearer, some present physics puzzles are expected to be solved. Quantum superfluid physical mathematical physical processing has considerable complexity, some rigorous proofs need further breakthroughs, and some of them are listed:
(1) It is meaningless to study the space-time of quantum superfluid, and the quantum topology of emergence excitation in its evolution process is the origin of space-time, as well as the origin of matter.
The quantum superfluid uniformly fills the whole universe, is the basic energy field of the universe, and it’s the driving force of the expansion of the universe. According to the current cosmological view, it is meaningless to study its space-time, which is relative. Its evolutionary process of EPT is quantum topology, which is the origin of space-time as well as the origin of matter.
(2) An important boundary from quantum superfluid state evolution to quantum state is the uncertainty relation
Here again, we need to emphasize that an important boundary from quantum superfluid state evolution to quantum state is the uncertainty relation. That is to say, it should be the condition for the localization of extremely thin, ultra-weak quantum superfluid into quantum states.
(3) Emergent excited with degenerate phase and intrinsic phase
In the literature, Ref. 2 extended the physics idea of “Time reversal” proposed by Feynman, a famous physicist, and believed that physical particles in human reality would have different “physical proper time” due to different periods in the evolution of the universe. Physical particles in reality should exist as the composite phase of degenerate phase and intrinsic phase; although such physical characterization may be difficult, it is understood why there are three generations of basic particles, we will look at this in detail in a subsequent article.
(4) Some physical concepts
EBSF spreads throughout the universe, and then randomly produces nodes that, in a universe above absolute 0K degree, may also have viscous properties (as observed in the superfluid). The developed resulting forms of this viscosity (plus homotopy topology type invariance) may be divided into gravitational, weak charge, color charge, and charge, which will be discussed in detail in the later papers. It is the main role of the universe’s expansion through the physical mechanism (still needs to be studied).
The quantum superfluid state produces photons, its velocity in physical space has not changed with the expansion of the universe, and is an eternal constant, which is very strange. For this reason, some scientists think that the propagation speed of photons is determined by the energy difference between the saddle point and the lowest concave point of the quantum superfluid energy in EBSF, therefore it does not change with the expansion of the universe. The light speed does not change from time to time and space to space, is easy to understand, and reflects the uniformity of the universe because there is no difference in the macrospace whose scale is less than or equivalent to the order parameter. Only under certain physical conditions does quantum superfluid evolve with mass properties. The main mechanism of “category sealing” is the ordering of quantum superfluid vortex lines or entanglement of quantum turbulence, which will be further investigated in subsequent papers.
(5) Physical state’s levels
Based on the physical view of the formation of the universe system, the idea of nonlinear evolution development, and the idea of level emergence theory in condensed matter physics, the author puts forward the preliminary framework of the hierarchy theory of physics. Quantum superfluid further evolves to quantum state (QCD, QED), in which the quantum topology physical state is an intermediate state; the macroscopic level that human can understand (the classical level of physics), further evolution to the special physical level suitable for the law of general relativity (super-macroscopic level).
While the physical level evolving, the field and gauge also change, which is more complex.
The main thread of the evolution of quantum superfluid states is the energy, the spatial scale and the resulting changes in physical state symmetry. The order parameter (coherence length) seems to reveal the inevitability of the evolution of quantum superfluid states into larger physical scale states.
According to the existing superfluid observations, the superfluid properties and nonlinear properties of quantum superfluid states seem to have memory under certain physical conditions.
(6) The physical nature of temperature
Temperature is a thermodynamic physical quantity, but it can be extended to the wave characterization of a wave phenomenon; on the one hand, it can reveal its physical nature, and on the other hand, it can characterize the gap energy of the evolution and development of quantum superfluid below absolute 0K.
8. Conclusion and Outlook
In summary, although we are still in the research stages, the study of quantum superfluid is new and difficult, and we can still preliminarily draw some conclusions:
| (1) | Researchers have carried out studies on tiny effects on fundamental particles with quantum vacuum about electroweak baryogenesis mechanism, we can further confirm the existence of the energy basic state field of the universe (EBSF). | ||||
| (2) | We propose that since EBSF is the basic energy field of the universe, quantum superfluid state must be the next level of fundamental particle (quantum state). Then, the evolution development equation of quantum superfluid state should be nonlinear, which can be expressed by the fraction fractal KdV equation temporarily. It is very important for later research. | ||||
| (3) | This paper reviews the experimental observation of superfluid in the existing physics, and puts forward the possible quantized form of KdV equation. One possible form of quantization for vortex line of quantum superfluid is the string theory, so the basic physical scenario and foundation of physics in string theory can be revealed, although this needs to be studied further in detail. | ||||
| (4) | Through the analysis of the KdV equation and general solution, the quantum superfluid state is the lowest level physical state in physics, and it is not uniform. There are common phenomena such as energy gap, non-closure and wrinkle (folding) in Euclidean space. We think this is the microscopic basis of the space-time of general relativity and it is very important for later research. | ||||
| (5) | Based on the physical view of the formation of the universe system, the idea of nonlinear evolution development, and the idea of level’s emergence theory in condensed matter physics, the author puts forward the preliminary framework of the Hierarchy Display Theory of physics: Quantum superfluid state further evolves to quantum state (QCD, QED), in which the quantum topology physical state is an intermediate state; the macroscopic level that humans can understand (the classical level of physics) requires further evolution to the special physical level suitable for the law of general relativity (super-macroscopic level of physics). | ||||
Quantum superfluid physics (or new physics) is new but has broad physical prospects, it uses the view and method of the whole universe and the system evolution, and the nonlinear development evolution and level’s emergence theory. It studies the evolution and development of quantum superfluid state under various physical conditions, the transformation and change of field gauge, and finally expounds the whole evolution and development of the physical hierarchy system and related physical laws and relations. In this process, the essence of some physics concepts is further clear, some present physics puzzles are expected to be solved. But some rigorous proofs need further breakthroughs, for example, how to derive the cosmological constant using the KdV equation and what are the physical conditions and procedures for the evolution of the KdV equations to general relativity. In addition, as pointed out in the paper, the KdV equation may only describe the normal evolution development state of EBSF, and cannot describe the generation of quantum turbulence, which is consistent with the normal fluid mechanics. These need to be studied in greater depth and in greater quantities.
Acknowledgments
The authors specially thank the unknown reviewer for his suggestions and to the editors for their hard work.
Conflict of Interests
The authors declare no conflict of interest. The authors have not received any funding or help or verbal encouragement from any organization or other people but are only interested in his research.


