Fractional hyper-chaotic system with complex dynamics and high sensitivity: Applications in engineering
Abstract
Hyper-chaotic systems have useful applications in engineering applications due to their complex dynamics and high sensitivity. This research is supposed to introduce and analyze a new noninteger hyper-chaotic system. To design its fractional model, we consider the Caputo fractional operator. To obtain the approximate solutions of the extracted system under the considered fractional-order derivative, we employ an accurate nonstandard finite difference (NSFD) algorithm. Moreover, the existence and uniqueness of the solutions are provided using the theory of fixed-point. Also, to see the performance of the utilized numerical scheme, we choose different values of fractional orders along with various amounts of the initial conditions (ICs). Graphs of solutions for each case are provided.
1. Introduction
The inquiry of hyperchaos is a concept based on chaotic dynamical systems. These systems have more complex dynamical behavior with at least two positive Lyapunov exponents compared with the chaotic system. Complex dynamics and high sensitivity of hyper-chaotic systems (HCS) have revealed the significance of such systems in communication technologies. These features were observed when the first were introduced.1,2,3 Owning at least four dimensions and a couple of unstable directions can be regarded as the main aspects of such systems. Many studies have been worked on such systems. For example, in Ref. 4, Chaotic digital cryptosystem has been reported. New parallel image encryption with chaotic windows was done in Ref. 5. Also. hyperchaotic attractor in a new hyperjerk model was studied in Ref. 6. Moreover, a novel hypersensitive hyperchaotic system equilibria have been studied in Ref. 7. Also, the fractional frame of a no-equilibrium hyperchaotic system can be seen in Ref. 8. Another study on a new 5D hyperchaotic system can be studied in Ref. 9. A new set of 4D hyperchaotic and chaotic systems with quadric surfaces was studied in Ref. 10. We consider a new hyper-chaotic system as follows11 :
Motivated by the aforesaid argument, the primary purpose of this study is to process a new and effective mathematical model for the hyper-chaotic system using fractional Caputo derivative (1) as
1.1. Nonstandard finite difference scheme (NFDS)
Now, we use the NFDS to get the approximate solutions of the considered system. The primary basis of the NFDS method comes from exact finite difference methods. These algorithms are well designed.40,41 Such methods are designed for recompensing deficiencies, for example for numerical instabilities that can be generated by standard finite difference schemes. With regard to the positiveness, boundedness, and monosyllabicity of solutions, NFDS methods own a more satisfactory application compared to the standard finite difference methods because of the adaptability that they own to create an NSFD method that is able to maintain certain features. Some applications of NFDS can be read in Refs. 42–48. We consider the following problem :
| (i) | Suppose un as the approximation of u(tn), so for (7) we have du(t)dt≈un+1−unϕ(h,ζ)(8) | ||||
| (ii) | Also, in a similar way for f(x(t),t,ζ), we have f(un+1,xn,…,t,ζ) un+1−unp(h,ζ)=f(un+1,un,…,t,ζ).(9) | ||||
We set p(h,ζ)=h for Eq. (8), a classic discretization can be derived, so (8) can be regarded as a generalization for its classic one. Moreover, the next consistency condition must be held with the denominator p(h,ζ) :
2. Numerical Method
Now we use the NSFD method presented in the previous section to show the results. Recall that Mickens suggested writing a general multistep numerical method to approximate the simulation of (7) by (9), where holds , and is a discretization . The examples of how the rules are employed to develop the discretization was reported in the previous section.49,50 Using the above-mentioned procedure, the next discretization can be written for (1)
So, from (18), the following relation can be obtained (1) :
3. Existence and Uniqueness
Now, we examine the existence and uniqueness of the solution of the considered fractional system employing the theory of fixed-point. Assume be a Banach space for the continuous real-valued functions on and with the norm , , , , . By employing the Caputo operator for relation (2), one can obtain
Theorem 3.1. The non-integer model (2) owns a unique solution with
Proof. As reported, , , and are bounded and , , and hold the Lipschitz condition. Hence, using and (32) we have
4. Results and Discussion
In this paper, we used an accurate nonstandard finite difference for the first time for solving a new noninteger hyper-chaotic system. Generating difference methods that preserve the stability behavior of the equilibrium points is crucial in numerical simulation. Now, we use the presented nonstandard finite difference to see the numerical behavior of the proposed fractional system. We show the accuracy and efficiency of the proposed numerical scheme for solving the studied fractional-order system under different fractional orders along with initial conditions. The values of parameters in the considered systems are as follows: , , , , , , , , and . We provide the approximate solutions of the system under different values of as and initial conditions and , , and by Fig. 1. Figure 1 shows how dependent variables behave under the selected orders. Figures 2 and 3 display the behavior of the solutions in 2D under the considered fractional orders using the numerical scheme reported in Sec. 2. Moreover, chaotic behaviors of the approximate solutions can be seen in Fig. 4.
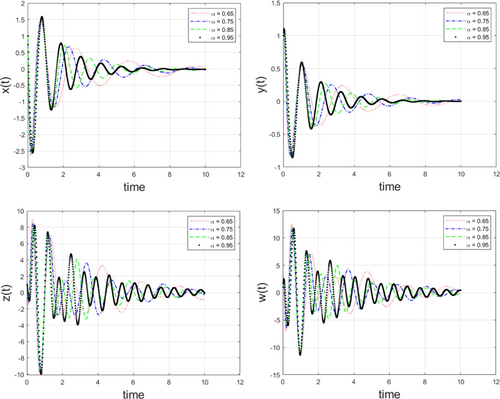
Fig. 1. (Color online) Approximate solutions for different values of as 0.65, 0.75, 0.85 and initial conditions 0.95 and , , and .
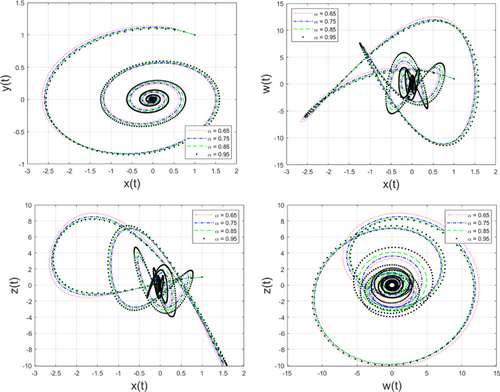
Fig. 2. (Color online) Approximate solutions for different values of as 0.65, 0.75, 0.85 and initial conditions 0.95 and , , and .
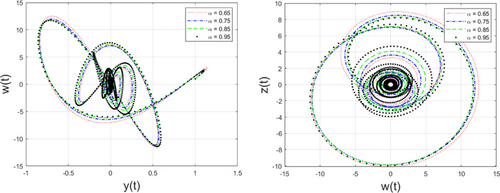
Fig. 3. (Color online) Approximate solutions for different values of as 0.65, 0.75, 0.85 and initial conditions 0.95 and , , and .
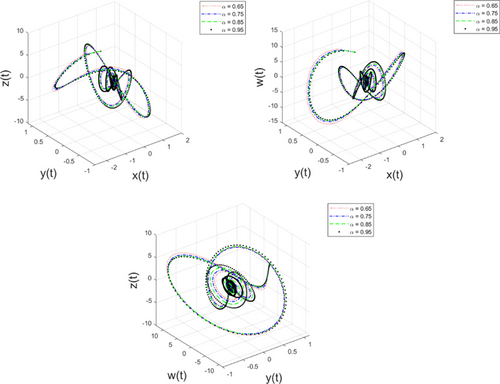
Fig. 4. (Color online) Approximate solutions for different values of as 0.65, 0.75, 0.85 and initial conditions 0.95 and , , and .
5. Conclusion
This work was dedicated to using the Caputo fractional derivative to design a new model for a new chaotic system. The existence and uniqueness of the solutions were provided successfully. Also, a numerical algorithm called a nonstandard finite difference scheme was used to obtain the approximate solutions. To see the performance of the suggested method, different values of initial conditions were considered and the solutions were shown through some figures. Also, to see how the studied fractional system behaves, we selected various amounts of fractional orders.
| Remember to check out the Most Cited Articles! |
|---|
|
Check out these titles in Condensed Matter Physics today! |


